Salut,
Je sais pas ce que c'est que
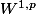
(et j'ai la flemme de chercher).
Par contre, un truc plus qu'archi classique, c'est que, si
)
est la boule de centre 0 et de rayon

de
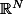
et que tu as une fonction
\rightarrow {\mathbb R})
telle que
)
ne dépende que de
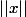
, c'est à dire telle que
\!=\!\varphi(||x||))
avec

alors on a :
}\!\!\!\!f(x)\,dx\!=\!C_N\big\int_{0}^{R}\varphi(\rho)\rho^{N-1}\,d\rho)
où

est une constante ne dépendant que de

(donc ni de R, ni de

) qui est en fait la "mesure (N-1)-dimensionnelle" de la sphère unité de
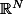
: (

= circonférence du cercle trigo ;

=surface de la sphère unité de R^3 . . .)
Et le résultat provient simplement d'un "passage en polaire" style

en dimension 2 ou
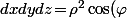\, d\rho\, d\varphi\, d\theta)
en dimension 3.
Modulo ce fait, ta question se ramène à une bête question sur les intégrales généralisées dans R.