Suite récurente d'une matrice

[Maths-ForumR]

Bonjour,

Soit (Un) la suite définie par :
Uo=1 ; U1=-1 ; U2=3
Un+3=-2Un + Un+1 + 2Un+2

1) On pose Xn=
Déterminer la matrice A telle que Xn+1=AXn
2) Réduire A et déduire Xn en fonction de n et Un en fonction de n.

Pour la 1) c'est bon
Pour la 2) on a Xn =A^n X0 mais comment trouver Un en fonction de n ?

Merci

[capitaine nuggets]

Salut !

Bonjour,

Soit (Un) la suite définie par :
Uo=1 ; U1=-1 ; U2=3
Un+3=-2Un + Un+1 + 2Un+2

1) On pose Xn=
Déterminer la matrice A telle que Xn+1=AXn
2) Réduire A et déduire Xn en fonction de n et Un en fonction de n.

Pouvez vous m'aider pour la 1 je suis bloqué
Pour la 2) on a Xn =A^n X0

Merci

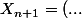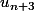
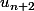
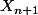
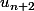
Pars de , puis remplace seulement par son expression en fonction de , et donnée dans l'énoncé. Tu auras alors écris comme matrice colonne dont les coefficients sont des combinaisons linéaires de , et . Il te suffira alors de reconnaître un produit matriciel de la forme , où est la matrice que tu cherches

[Maths-ForumR]

Merci j'ai trouvé :
A=0 1 0 // 0 0 1 // -2 1 2 (en ligne)

Savez vous se que signifie réduire la matrice A je ne comprend pas, je dois la diagonaliser ?

[zygomatique]

salut

peut-être pas la diagonaliser (ce qui n'est pas toujours possible)... mais surement la rendre triangulaire ...