Bonjour à tous
Je bloque actuellement sur un DM portant sur les coefficients binomiaux
Voici les questions sur lesquelles je bloque :
"Les coefficient binomiaux sont les nombres, ( n / p )ou n et p sont des entiers vérifiant, 0<=p<=n, défini par ;
( n / p )= n!/(p!(n-p)!)
1. Démontrer que pour tout entier entier naturels p et k :
Somme de ( n p ) pour n allant de p à p+k = ( p+1+k / p+1 ).
2.a. Donner 3 polynômes P0, P1 et P2 tels que pour tout entier p compris entre 0 et 2 et tout entier n>=p.
Pp(n) = ( n / p )
b. Déterminer trois nombre α0, α1, α2 tels que pour tout réel x :
x² = Somme de αp*Pp(x) pour p allant de 0 à 2.
c. En déduire un polynôme, S2 tel que pour tout entier naturel, n :
Somme de k² pour k allant de 0 à n = S2(n)"
Pour 2.a j'ai trouvé que p0(n) serait égal à 1 car lorsque p = 0, ( n / p )= 1 mais je ne sais pas trouver le polynôme ensuite.
Puis j'ai trouvé P1(n)=n et P2(n)= ( n-1 / p ) + ( n-1 / p-1 ) mais pareil je reste bloqué
Merci
DM Maths TS coefficient binomiaux
9 messages
- Page 1 sur 1
Re: DM Maths TS coefficient binomiaux
Bonsoir,
A mon avis, tu peux simplifier ta formule de P2(n) en repartant de la définition des coefficients binomiaux.
Ensuite, par exemple, quel est le polynôme P1 tel que P1(n) = n pour tout n ?
A mon avis, tu peux simplifier ta formule de P2(n) en repartant de la définition des coefficients binomiaux.
Ensuite, par exemple, quel est le polynôme P1 tel que P1(n) = n pour tout n ?
Re: DM Maths TS coefficient binomiaux
Comme ( n / p ) + ( n / p+1 ) = ( n+1 / p+1 ) alors P2(n) = ( n-1 / p-1 ) + ( n-1 / p ) = ( n / p ) ?
Pour P1, le polynôme 2n-n ? Mais il serai égal à n ce qui revient à dire n = n. Ça semble bête mais je ne trouve pas
Pour P1, le polynôme 2n-n ? Mais il serai égal à n ce qui revient à dire n = n. Ça semble bête mais je ne trouve pas
Re: DM Maths TS coefficient binomiaux
P2(n) = ( n / 2) tout simplement = .... ??
Je t'aide, P1(n) = n, donc le polynôme cherché est : P1(x) = x.
Je t'aide, P1(n) = n, donc le polynôme cherché est : P1(x) = x.
Re: DM Maths TS coefficient binomiaux
Désolé mais je ne comprend juste pas comment je peux parvenir à un polynôme avec ces expressions là ?
Re: DM Maths TS coefficient binomiaux
Il faut trouver 3 polynômes différents.
P0(n) = 1 pour tout n. Le polynôme P0 tel que P0(x)=1 vérifie cette relation : P0(n) =1 pour tout n. Dans cette question, on ne demande pas plus de donner un polynôme qui fonctionne.
En fait on démontre qu'il n'en existe qu'un seul (qui prend des valeurs données pour un nombre infini d'éléments), mais ce n'est pas au programme de TS.
P0(n) = 1 pour tout n. Le polynôme P0 tel que P0(x)=1 vérifie cette relation : P0(n) =1 pour tout n. Dans cette question, on ne demande pas plus de donner un polynôme qui fonctionne.
En fait on démontre qu'il n'en existe qu'un seul (qui prend des valeurs données pour un nombre infini d'éléments), mais ce n'est pas au programme de TS.
Re: DM Maths TS coefficient binomiaux
D'accord merci, vous auriez des pistes pour les autres questions ? Je bloque aussi.
Re: DM Maths TS coefficient binomiaux
As-tu trouvé P0, P1 et P2 ?
b) Ensuite il faut trouver tels que
tels que 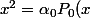 + \alpha_1 P_1(x) + \alpha_2 P_2(x)) pour tout x.
pour tout x.
Cela se fait par identification sur les coefficients des 2 polynômes à droite et à gauche du signe égal.
b) Ensuite il faut trouver
Cela se fait par identification sur les coefficients des 2 polynômes à droite et à gauche du signe égal.
Re: DM Maths TS coefficient binomiaux
Pas encore, à vraie dire, j'ai du mal à comprendre le rôle de (n) dans P0(n) mais là, il faut que je dorme, je continuerai de chercher demain, merci.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
