Tu peux remarquer que
Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+1)
7 messages
- Page 1 sur 1
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
Bonjour
Tu peux remarquer que) est une primitive de
est une primitive de 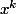 .
.
Tu peux remarquer que
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
Tu peux utiliser le fait que la dérivée de la somme demandée est 
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
Oui, tu dois trouver la primitive qui convient pour ta somme initiale.
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
J'ai rajouté les balises TEX, et je ne vois pas trop où est ton problème. J'appelle
On en était à
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
Salut,
C'est peut-être un soupçon plus long à écrire (vu qu'il il faut recopier les signe intégrales à toutes les étapes), mais on peut aussi écrire directement que :
\Big]<br />=\int_0^x\Big[\sum_{k=0}^n{k\choose n}t^{k}\Big]dt<br />=\int_0^x(t\!+\!1)^n dt<br />=\Big[\frac{(t+1)^{n+1}}{n+1}\Big]_0^x\!\!<br />=\dfrac{(x\!+\!1)^{n+1}\!-\!1}{n+1})
C'est évidement parfaitement totalement exactement la même chose qu'en dérivant / intégrant, sauf que ça évite d'avoir à gérer les constantes d'intégration vu qu'elle "coulent de source" en procédant de la sorte.
C'est peut-être un soupçon plus long à écrire (vu qu'il il faut recopier les signe intégrales à toutes les étapes), mais on peut aussi écrire directement que :
C'est évidement parfaitement totalement exactement la même chose qu'en dérivant / intégrant, sauf que ça évite d'avoir à gérer les constantes d'intégration vu qu'elle "coulent de source" en procédant de la sorte.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
Bonsoir,
sinon, une méthode directe de calcul existe en utilisant la formule
et avec une réindexation de la somme
sinon, une méthode directe de calcul existe en utilisant la formule
et avec une réindexation de la somme
Re: Somme de coefficients binomiaux k parmis n * x^(k+1)/(k+
La fonction  est une fonction polynômiale définie sur
est une fonction polynômiale définie sur  . On a le droit de regarder
. On a le droit de regarder ) pour tout
pour tout 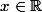 . Comme
. Comme ) s'annule en
s'annule en  , c'est une valeur très commode. Mais on peut prendre autre chose!
, c'est une valeur très commode. Mais on peut prendre autre chose!
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
