Ktsfer a écrit:b°/ etudier le sens de variation de la suite (decroissante sur 0;1/2 et croissante sur 1/2 ; + l'infini
Avant d'avancer à la question c), il faudrait déjà corriger la question b) !
Tu as défini la fonction
=kx(1-x))
(sans le dire !) pour pouvoir écrire
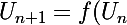)
. Pourquoi pas ? Mais, il ne faut pas confondre pour autant la suite et la fonction. f est croissante sur

, et décroissante sur

, mais cela n'est pas la même chose que
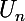
. Étudier la croissance d'une suite, c'est dire comment varient les termes successifs
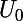
,
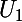
,
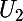
,...Et tu n'as pas répondu à la question ! (Je suppose que tu parlais de la croissance de f, mais de toutes manières, si c'est le cas, tu t'es trompé sur la croissance de f !)
De fait, si k=1, la suite s'écrit :
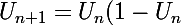)
et par conséquent
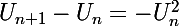
, ce qui veut dire que tant que
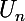
n'est pas nul, la suite est décroissante !
Ktsfer a écrit:c°/demontrer que pour tout entier naturel n : 0<un<1
alors j'ai calculé f(1/2) = 1/2(1 - 1/2) = 1/4
donc j'en déduit que un<1 mais la je trouve pas comment faire pour demontrer que 0<un
Je ne vois pas l'intérêt de calculer f(1/2). Je ne vois pas non plus en quoi le fait que f(1/2)=1/4 te permet d'affirmer que 0<Un pour tout entier naturel !
En calculant f(1/2) tu as simplement démontré que si
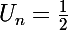
(ce qui ne se produira jamais, d'ailleurs !) alors
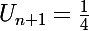
.
Tu dois trouver un moyen de démontrer que

quel que soit n ! Tant que tu n'auras pas fait cela, tu n'auras pas répondu à la question !
