Géométrie dans l'espace

[Angelol]

Bonjour, je suis actuellement en bts design et notre professeur nous a donné un dm de maths. Je n'arrive pas à répondre à la derniere question..
Les consignes sont :
ABCDEFGH est un cube d'arête a :
1) définir la nature puis calculer le périmètre et l'aire EBG (ça c'est facile, j'ai réussi)
2) nature et volume de FEBG
3) Soit M le centre de BEG. Calculer la longueur FM (là j'ai trouvé a racine de 1 tier)
4) les points F, M et D sont-ils alignés ?

Je n'arrive pas à répondre à la 4, pouvez vous m'aider s'il vous plaît ?

[XENSECP]

Salut,
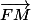
Personnellement je mettrais les points dans un repère. Ensuite il suffit de montrer que et sont colinéaires par exemple.

[Angelol]

Merci pour votre réponse, le problème c'est que je n'ai aucune idée de comment le faire, et je n'arrive pas à trouver les coordonnées de M

[siger]

correction

[chan79]

salut
ou peut-être montrer que (FM) et (FD) sont toutes les deux perpendiculaires au plan BEG, c'est juste une idée

[Ben314]

Salut,
Juste pour vérifier que tout le monde est sur la même longueur d'onde : ABCD c'est une des face du cube (dont le périmètre peut être parcouru dans cet ordre) et [AE], [BF], [CG], [DH] sont des arrêtes du cube ?

(Je suppose que toi tu as un dessin, nous on l'a pas et j'ai jamais entendu dire qu'il y avait une façon canonique de nommer les sommets d'un cube...)

[Angelol]

Salut,
Juste pour vérifier que tout le monde est sur la même longueur d'onde : ABCD c'est une des face du cube (dont le périmètre peut être parcouru dans cet ordre) et [AE], [BF], [CG], [DH] sont des arrêtes du cube ?

(Je suppose que toi tu as un dessin, nous on l'a pas et j'ai jamais entendu dire qu'il y avait une façon canonique de nommer les sommets d'un cube...)

Oui c'est exactement ça !

[siger]

bonsoir

3) sauf erreur je trouve FM = V(2)/2 et non V(3)/3 ....a voir!
4) tu connais les coordonnees de G (par exemple) et celle du milieu K de EB
M est le centre de gravité de BEG (equilateral) donc au 2/3 de KG
........
remarque :
dans le plan BDHF on porte L milieu de FH et P intersection de FD avec DL
les droites F(L)H et BD etant paralleles on montre que FL/BH= LP/PB= 1/2
d'ou BP/LP = 2/3
Le point P situé au 2/3 de la mediane BL du triangle BEG est donc confondu avec le point M
....

[chan79]

F est équidistant de B, E et G.
M est équidistant de B, E et G.
D est équidistant de B, E et G.
F, M et D sont donc tous les trois situés sur la droite intersection des 3 plans médiateurs de [BE], [EG] et [BG]. Ils sont donc alignés.

[Pseuda]

Bonsoir,

Il y a plusieurs façons de résoudre le problème. Tout dépend des notions que tu as l'habitude de manipuler :

- coordonnées dans un repère ?
- barycentre ? --> pour trouver les coordonnées de M
- plan médiateur ?
- orthogonalité dans l'espace ?

Les 2 dernières, si tu les connais, te permettront de résoudre le problème.

Oups, trop tard, je laisse mon message.

[Ben314]

Il y a effectivemnt des tas de façon de montrer que F, M et D sont alignés.
- Celle demandant sans doute le moins de réflexion consiste à se placer dans un repère (on remplace le raisonnement par du calcul).
- Plusieurs méthodes un peu plus géométrique comme celle de siger ou encore celle là :
M étant le "centre" du triangle (BEG), il est à l'intersection des médianes du triangles, donc en particulier sur la droite (BL) où L est le milieu de [EG] donc aussi le milieu de [FH] vu que (EFGH) est un carré (donc un parallélogramme dont les diagonales se coupent en leur milieu).
Les droites (BF) et (DH) étant parallèles, elles sont contenues dans le même plan (BFD). Ce plan contient B et le milieu L de [FH] donc la droite (BL) donc il contient le point M.
Le même raisonnement montre que M est aussi dans le plan (GFD) donc il est en fait sur l'intersection des deux plans, c'est à dire sur la droite (DF).
- Enfin, la méthode qui me semble la plus simple, c'est d'utiliser un argument de symétrie :
Si on fait tourner le cube d'un tiers de tour autour de l'axe (DF), les points B,G,E se retrouvent respectivement en G,E,B ce qui montre que le centre M du triangle (BGE) n'a pas bougé et donc qu'il est sur l'axe de la rotation.