bonjour à tous,
dans un exercice on me demande de montrer que sin x + siny + sin z - sin (x+y+z) = 4sin (x+y/2)sin(y+z/2)sin(z+x/2)
J'ai essayer de simplifier avec la formule sin x + sin y = 2sin (x+y/2)cos(x-y/2) , mais je me retrouve rapidement bloquer...
merci d'avance de vos msg
Trigonométrie
7 messages
- Page 1 sur 1
Re: trigonométrie
Salut,
2 sin((x+y)/2)sin((y+z)/2) = - cos(y + (x+z)/2) + cos((x-z)/2)
et ensuite tu multiples par 2sin((z+x)/2) et tu développes et tu as ton résultat en utilisant la formule 2sinacosb = sin(a+b) +sin(a-b)
à vérifier et pense à rajouter des parenthèses comme te le signale Kolis
2 sin((x+y)/2)sin((y+z)/2) = - cos(y + (x+z)/2) + cos((x-z)/2)
et ensuite tu multiples par 2sin((z+x)/2) et tu développes et tu as ton résultat en utilisant la formule 2sinacosb = sin(a+b) +sin(a-b)
à vérifier et pense à rajouter des parenthèses comme te le signale Kolis
Re: trigonométrie
Merci beaucoup, je vais essayer avec ça mais est ce que tu pourrais m'indiquer comment tu as trouver ton égalité stp
Re: trigonométrie
Bonjour,
D'abord on utilise la formule : + \sin(b) = 2 \sin(\frac{a+b}{2}) \cos(\frac{a-b}{2})) , qui donne :
, qui donne :
 + \sin(y) = 2 \sin(\frac{x+y}{2}) \cos(\frac{x-y}{2}))
et - \sin(x+y+z) = \sin(z) + \sin(-x-y-z)= 2 \sin(\frac{z-x-y-z}{2}) \cos(\frac{z+x+y+z}{2}))
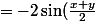 \cos(z+\frac{x+y}{2})) ,
,
donc + \sin(y) + \sin(z) - \sin(x+y+z))
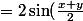(\cos(\frac{x-y}{2})-\cos(z+\frac{x+y}{2})))
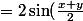 ( 2\sin(\frac{x-y+2z+x+y}{4}) \sin(\frac{2z+x+y-x+y}{4}))) : par la formule donnée par M.Jlb
: par la formule donnée par M.Jlb
\sin(\frac{x+z}{2})\sin(\frac{y+z}{2})) .
.
D'abord on utilise la formule :
et
donc
Re: trigonométrie
Merci beaucoup, j'étais arrivé à peu près là, mais une erreur dans mon calcul m'empêchais de trouver le bon résultat, en tout les cas merci j'ai compris où étais mon erreur
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
