Suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zartos
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Aoû 2016, 21:37
-
 par zartos » 29 Aoû 2016, 01:19
par zartos » 29 Aoû 2016, 01:19
Bonsoir,
(Un): U0=
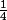
et Un+1=f(Un).
f(x)= (2-

)²
J'ai du mal à calculer U2n et U2n+1.
Merci d'avance
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 29 Aoû 2016, 01:54
par Razes » 29 Aoû 2016, 01:54
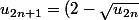^2=(2-\sqrt{(2-\sqrt{u_{2n-1}})^2})^2)
Simplifie, Que peux tu constater?
-
zartos
- Membre Naturel
- Messages: 10
- Enregistré le: 28 Aoû 2016, 21:37
-
 par zartos » 29 Aoû 2016, 02:10
par zartos » 29 Aoû 2016, 02:10
Razes a écrit: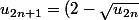^2=(2-\sqrt{(2-\sqrt{u_{2n-1}})^2})^2)
Simplifie, Que peux tu constater?
Salut Razes, merci pour ta réponse mais pourquoi remplacer U2n sous la racine par[2-√(U2n-1)]²
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 29 Aoû 2016, 10:53
par Razes » 29 Aoû 2016, 10:53
Tente au moins de le faire.
Calcule

et
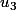
Que constates tu?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Aoû 2016, 11:57
par zygomatique » 29 Aoû 2016, 11:57
salut
zartos a écrit:Bonsoir,
(Un): U0=
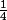
et Un+1=f(Un).
f(x)= (2-

)²
J'ai du mal à calculer U2n et U2n+1.Merci d'avance
moi aussi ... car cette consigne ne veut rien dire ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 29 Aoû 2016, 12:02
par Razes » 29 Aoû 2016, 12:02
Razes a écrit:Tente au moins de le faire.
Calcule

et
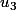 Que constates tu
Que constates tu?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Simplifie, Que peux tu constater?
et Un+1=f(Un).
)²