f(x,y) =
Fonction a deux variables
4 messages
- Page 1 sur 1
Re: fonction a deux variables
Cherche les points critiques en calculant :
=0) et
et =0)
En principe tu dois trouver 4 points et il faudrait déterminer si ce sont des extremum locaux ou non.
En principe tu dois trouver 4 points et il faudrait déterminer si ce sont des extremum locaux ou non.
Re: fonction a deux variables
Bonjour,
On a = 3 x (x+2)) et
et  = 3 y (y- 2)) ,
,
donc = 0 \Rightarrow x\in \{0,-2\}) et
et  = 0 \Rightarrow y\in \{0,2\}) .
.
Soit E l'ensemble des points qui sont candidats à être des extremums locaux ,
donc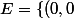 ; (0,2) ; (-2,0) ; (-2,2) \}) .
.
On calcule maintenant) ,
, ) et
et ) : on a
: on a  = \frac{\partial^2f}{\partial y \partial x}(x,y)) car
car  .
.
et pour chaque point\in E) , on pose :
, on pose : 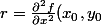 , t = \frac{\partial^2f}{\partial y^2}(x_0,y_0)) ,
,
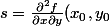 et \mathcal D = s^2 - rt) .
.
On a un théorème qui dit :
*) si et
et  on a un maximum local au point
on a un maximum local au point ) ,
,
**) si et
et 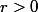 on a un minimum local au point
on a un minimum local au point ) ,
,
***) si 0 on n'a ni maximum local ni minimum local au point
0 on n'a ni maximum local ni minimum local au point ) : on a un point col .
: on a un point col .
Pour les extremums globaux , leur étude est simple pour ce cas .
Je crois que vous avez tous les ingrédients nécessaires pour nous faire une belle solution de cet exercice .
Bon courage.
On a
donc
Soit E l'ensemble des points qui sont candidats à être des extremums locaux ,
donc
On calcule maintenant
et pour chaque point
On a un théorème qui dit :
*) si
**) si
***) si
Pour les extremums globaux , leur étude est simple pour ce cas .
Je crois que vous avez tous les ingrédients nécessaires pour nous faire une belle solution de cet exercice .
Bon courage.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
