Merci d'avoir répondu ^^
En fait pour l'exponentielle, ce que je veux dire, c'est que n'importe quelle fonction exponentielle (y compris celle de base e) n'est pas définie pour les irrationnels, où l'on ne peut pas calculer la valeur.
En fait,
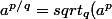)
(certes, je sais pas comment on fait la racine q-ième...) avec p un entier relatif et q un entier naturel et donc j'ai l'impression qu'avec un irrationnel, on ne pourrait pas calculer normalement la valeur et qu'on calcule juste une valeur inexacte en utilisant un rationnel proche de l'irrationnel (par exemple pour
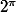
on calculerait en gros 2 à la puissance

).
Et donc je me demande si on considère que les fonctions exponentielles sont malgré tout définies sur

parce que ça me parait bizarre...
(En espérant avoir été plus clair...)
Edit : En fait avec la formule qui remplace l'exponentielle de base a (a réel strictement positif) par l'exponentielle de base e, c'est censé pallier le problème, mais c'est que je ne vois pas pourquoi la fonction exponentielle de base e serait définie sur

...
Est-ce que la fonction exp est définie comme étant la seule fonction dont la dérivée vaut elle même et qui prend la valeur 1 en 0 ou alors elle est définie comme la fonction exponentielle de base e qui vaut environ 2,718 ? Parce que dans le deuxième cas elle est définie sur
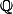
...
