Vocabulaire (Limite/Tendance/Convergence)

[KarnaZushin]

Bonjour.

Situation simple, j'ai une fonction constante (disons, pour x réel, f(x)=3)
Evidemment, la limite de ma fonction en +l'infinie est de 3

Pour autant, est-ce que je peux dire que ma fonction "tend" ou "converge" vers 3 ?
Ou est-ce que ces termes impliquent nécessairement le fait de se rapprocher de la valeur (ici 3) sans jamais l'atteindre ?

[catamat]

Bonjour

Le terme exact est celui de limite, la limite de f quand x tend vers +inf est égale à 3.

Dans la définition formelle de la limite on doit avoir |f(x)-3| aussi petit que possible à condition de choisir x suffisamment grand (ceci avec un epsilon qui pourra être choisi petit et un A qui lui pourra être grand)...
donc rien n'empêche d'avoir f(x)-3=0.

[KarnaZushin]

Bonjour

Le terme exact est celui de limite, la limite de f quand x tend vers +inf est égale à 3.

Dans la définition formelle de la limite on doit avoir |f(x)-3| aussi petit que possible à condition de choisir x suffisamment grand (ceci avec un epsilon qui pourra être choisi petit et un A qui lui pourra être grand)...
donc rien n'empêche d'avoir f(x)-3=0.

Bonjour, merci de ta réponse
Mais je ne suis pas sûr de comprendre la réponse qu'elle donne à mon problème.
On est bien d'accord que ma question porte sur la possibilité d'utiliser les termes "converger" ou "tendre" dans ce genre de situation ? en aucun cas le calcul de la limite n'est le problème ici.

[phyelec]

Bonjour,
Voici quelques éléments de réponses :
Les limites sont étudiées soit en un point soit en +/-
Si la limite d'une fonction existe en un point alors on dit qu'il y a convergence de la fonction en ce point.
Si une suite converge vers un réel L (la définition dit unique). Ce réel L est appelé la limite de la suite ou de la fonction.

Intuitivement la notion de "tend vers" une valeur L signifie que une fonction se rapproche de L quand tend vers ou +/- sans pour autant l'atteindre.

Autre manière de dire :
Soit un réel et f une fonction définie au voisinage de , sauf peut-être en , et à valeurs dans R. Soit L un réel. On dit que f tend vers L quand tend vers , ou que f a pour limite L en si

Si la limite L est atteinte quand tend vers et vaut alors f est continue en .

[hdci]

Pour précision, "converge vers" sera réservé à une limite finie. La limite peut exister tout en étant infinie (exemple la fonction 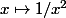) mais on ne dira pas que la fonction converge.

[KarnaZushin]

Soit un réel et f une fonction définie au voisinage de , sauf peut-être en , et à valeurs dans R. Soit L un réel. On dit que f tend vers L quand tend vers , ou que f a pour limite L en si .

Donc, selon cette définition, on peut ici dire que f(x) "tend" vers 3 quand x tend vers +l'infinie malgré l'absence de notion de "rapprochement".
C'est ça ?

[KarnaZushin]

A NOTER :
Le type de réponse que j'attends :

Soit : "On peut bien ici dire que f(x) "converge" ou "tend " vers 3 (même s'il l'on a pas de notion de rapprochement comme ces termes l'impliqueraient intuitivement, elle n'est en réalité pas nécessaire à l'utilisation de ces termes)"

Soit : "Non, on ne peut pas ici dire que f(x) "converge" ou "tend" vers 3 car la terminologie "tendre vers" ou "converger vers" ne signifie pas seulement que la limite de la fonction est égale à la valeur indiquée mais plus précisément encore que (...)"

[phyelec]

Il n'y a pas de notion de "on peut dire", on dit ou on ne dit pas.


Si la limite existe quand tend vers ( c'est à dire se rapproche de ) alors on dit qu'il y a convergence, donc dans le cas de la fonction constante f(x)=3, la limite existe en (dans ce cas la fonction vaut toujours la même chose quand on se rapproche de ) de donc il y a convergence vers cette limite.

[phyelec]

Complément .

Si la limite L d'une fonction existe quand tend vers (c'est à dire quand se rapproche de ) alors on dit que la fonction "convergence vers L " ou "tend vers L", ou "a pour limite L" quand quand tend vers .

[mathelot]

bonsoir,
si la fonction f constante sur R, égale à 3 ( f(x)=3 pour x réel) , on peut dire que f tend vers 3 quand x tend vers +oo