Suites Terminale S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jchntls
 par Jchntls » 02 Aoû 2016, 19:15
par Jchntls » 02 Aoû 2016, 19:15
Bonjour,
j'ai un problème avec un exrcice d'anabac. Le livre me donne la réponse mais pas le détail.
Il faut prouver que la suite wn est décroissante.
wn=n/3^n
La réponse est (1/3^(n+1))x(1-2n)
Il faut faire avec la formule w(n+1)-wn, ce que j'ai fais, mais je n'arrive pas à faire apparaître le -2n
Merci pour votre aide

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 02 Aoû 2016, 19:22
par Razes » 02 Aoû 2016, 19:22
Calcule
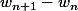
avec une factorisation

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Aoû 2016, 19:53
par zygomatique » 02 Aoû 2016, 19:53
salut
Il faut prouver que la suite wn est décroissante.
wn=n/3^n
La réponse est (1/3^(n+1))x(1-2n)
qu'est-ce que ce charabia ?
la réponse à quoi ?
Il faut faire avec la formule w(n+1)-wn
idem ... qu'est-ce que ça veut dire ?
si w_n = n/3^n il semble plus judicieux de calculer

puisque les termes sont positifs ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
medomar
- Messages: 5
- Enregistré le: 02 Aoû 2016, 19:50
-
 par medomar » 02 Aoû 2016, 20:03
par medomar » 02 Aoû 2016, 20:03
w(n+1) - w(n)= n+1/3^n+1 - n/3^n = (n+1-3n)/3^n+1=(1-2n)/3^n+1 <=0 pour n>=1/2
juste un petit calcul a ne pas faire w(n+1)/w(n)
ca donne pas de résultat
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 02 Aoû 2016, 20:28
par Razes » 02 Aoû 2016, 20:28
Tu as raison medomar, D'ailleurs j'avais demandé à Jchntls de faire le calcul, mais il n'a pas répondu. En tout cas c'était pas du charabia.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Aoû 2016, 11:33
par zygomatique » 03 Aoû 2016, 11:33
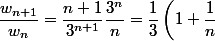 \le \dfrac 1 3 (1 + 1) \le \dfrac 2 3)
donc la suite est décroissante ....
et l'énoncé est un charabia ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 03 Aoû 2016, 18:35
par Razes » 03 Aoû 2016, 18:35
Bonjour zygomatique,
zygomatique a écrit: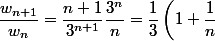 \le \dfrac 1 3 (1 + 1) \le \dfrac 2 3)
donc la suite est décroissante ....
et l'énoncé est un charabia ...
Oui, car la suite est positive. J'ai fait ça en premier mais ceci ne répondait pas à la demande de
Jchntls qui avait la réponse de l'exercice mais n'obtenait pas la même chose et ceci en partant du calcul de

.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Aoû 2016, 19:05
par zygomatique » 03 Aoû 2016, 19:05
j'ai dit dans mon premier post que la suite est positive ....

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 03 Aoû 2016, 19:38
par Razes » 03 Aoû 2016, 19:38
@zygomatique
J'avais vu et je l'ai réécrit instinctivement par ce que c'est important. Tant mieux pour Jchntls , il saura ainsi qu'il y a une autre façon pour prouver la convergence.
Concernant ce que voulait Jchntls , je pense que tu es d’accord?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Aoû 2016, 10:35
par zygomatique » 04 Aoû 2016, 10:35
mais bien sur ... bien qu'on n'ait plus de nouvelle de lui ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 161 invités
