Bonjour à tous!
J'ai le graphique ci-joint.
On me demande le nombre de solution(s) tel(s) que g'(x)=0
Je cherche donc les endroits où la tangente à la courbe est horizontale, je trouve g'(-4)=g'(0)=g'(6)=0
Le sujet est un QCM, on me propose les réponses: 0, 1, 2 ou 3. Je répond donc 3 mais il semblerait que ce soit faux, la réponse serait 1, j'ai beau me creuser la tête, chercher des interprétations graphique d'une dérivée nulle en un point etc, j'en viens au même résultat, je trouve 3 points tels que g'(x)=0.
J'aimerai qu'on m'explique où est-ce que je fais fausse route, ou mieux, qu'on me confirme qu'il y a une erreur dans la correction du sujet.
Merci à vous.
Lecture graphique
12 messages
- Page 1 sur 1
Lecture graphique
- Fichiers joints
-
- 2012-12-03_09_27_50-maths2012.pdf_-_adobe_reader_663.jpg (115.09 Kio) Vu 366 fois
Re: Lecture graphique
Salut,
Si tu dois te fier à la représentation graphique de la fonction, alors tu vois que la fonction n'est pas dérivable ni en 0, ni en 6, bien qu'elle y soit continue. Elle est par contre dérivable à droite et à gauche en ces points-là, même si les dérivées calculées à gauche et à droite n'ont pas la même valeur...
Cela ne semble pas évident, et on pourrait imaginer qu'en zoomant un peu, il pourrait y avoir une pente nulle en ces points. Mais il ne faut pas pousser le vice à l'extrême.
Si tu dois te fier à la représentation graphique de la fonction, alors tu vois que la fonction n'est pas dérivable ni en 0, ni en 6, bien qu'elle y soit continue. Elle est par contre dérivable à droite et à gauche en ces points-là, même si les dérivées calculées à gauche et à droite n'ont pas la même valeur...
Cela ne semble pas évident, et on pourrait imaginer qu'en zoomant un peu, il pourrait y avoir une pente nulle en ces points. Mais il ne faut pas pousser le vice à l'extrême.
Re: Lecture graphique
Salut,
En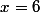 , si tu traces les tangentes à droite et à gauche tu verras qu'elles ne sont pas les mêmes. En fait ta fonction ne semble pas dérivable en
, si tu traces les tangentes à droite et à gauche tu verras qu'elles ne sont pas les mêmes. En fait ta fonction ne semble pas dérivable en 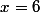 (ce qui se voit à la courbe "pointue"). Je pense qu'il se passe la même chose en
(ce qui se voit à la courbe "pointue"). Je pense qu'il se passe la même chose en  et c'est pourquoi il n'y a qu'en
et c'est pourquoi il n'y a qu'en 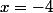 que l'on a une tangente horizontale.
que l'on a une tangente horizontale.
Après je te l'accorde, ce n'est pas évident à voir sur un graphique. Est-ce que tu n'as que ce graphique ou bien aussi une expression analytique de ?
?
En
Après je te l'accorde, ce n'est pas évident à voir sur un graphique. Est-ce que tu n'as que ce graphique ou bien aussi une expression analytique de
Re: Lecture graphique
Je ne vois pas comment tu fais pour voir que les tangentes ne sont pas les mêmes à droite et à gauche, Je n'ai que le graphique. J'ai l'impression qu'on a des tangentes identiques autour de 0 plus qu'autour de 4?
Peut-être que les questions d'avant aident à trouver le résultat: on nous demande l'équation réduite de D (: y=(1/2)x-1 ), la limite en plus infini de g(x)-2.5 (:-5) et g'(4) (:-(3/2))?
Peut-être que les questions d'avant aident à trouver le résultat: on nous demande l'équation réduite de D (: y=(1/2)x-1 ), la limite en plus infini de g(x)-2.5 (:-5) et g'(4) (:-(3/2))?
Re: Lecture graphique
sazer a écrit:Je ne vois pas comment tu fais pour voir que les tangentes ne sont pas les mêmes à droite et à gauche, Je n'ai que le graphique. J'ai l'impression qu'on a des tangentes identiques autour de 0 plus qu'autour de 4?
Peut-être que les questions d'avant aident à trouver le résultat: on nous demande l'équation réduite de D (: y=(1/2)x-1 ), la limite en plus infini de g(x)-2.5 (:-5) et g'(4) (:-(3/2))?
Bonjour,
Je pense que l'on peut voir les choses comme cela : http://www.cjoint.com/c/FEDodrJBJ57
Re: Lecture graphique
laetidom a écrit:Bonjour,
Je pense que l'on peut voir les choses comme cela : http://www.cjoint.com/c/FEDodrJBJ57
Jolis dessins ♥
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Lecture graphique
Merci Lostounet !, et oui j'ai pensé qu' "un dessin valait peut-être mieux qu'un long discours" dans ce cas . . . Bonne journée malgré la pluie !
@ sazer : content que mon dessin ait pu t'aider à visualiser ce que nos collègues avaient commencé à t'expliquer !
@ sazer : content que mon dessin ait pu t'aider à visualiser ce que nos collègues avaient commencé à t'expliquer !
Re: Lecture graphique
Sake a écrit:Beaux dessins en effet, Laetidom !
Simple et efficace
Merci Sake ! en effet, après vos bonnes explications détaillées, j'ai pensé que seul un bon visuel pouvait transformer l'essai ==> Nous avons réussi, c'est super !
Bonne journée.
Re: Lecture graphique
sazer a écrit:Oui bien sûr, bon travail d'équipe!
C'est l'esprit du forum, quand on peut et que le résultat est là, c'est gratifiant pour tous ! @+ sur le forum.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
