Bonjour à tous
Je bute sur un exercice sur les complexes.
On a z'=(z-1)/(z+2)
On veut les points M tels que z'=-(z')*
Voici ce que j'ai fait :
-(z')* = -(z*-1) / (z*+2)
Je bloque dans les développements ça ne me mène nulle part.
( je précise: z est l'affixe de M et z* = z barre = conjugué de z )
Géométrie complexe
10 messages
- Page 1 sur 1
Re: Géométrie complexe
remplace z' par son expression, et mets l'équation sous la forme ? zz* + ?z + ?z* + ? = 0.
Re: Géométrie complexe
Merci,
z'=((z*-1)(z+2))/((z*+2)(z+2)) mais ensuite j'ai un quotient z'=(zz*-z-2)/(zz*+2(z+z*)+4)
Je sais aussi que zz*=x²+y² mais je vais partout sauf au bon endroit avec tout ça.
L'exercice est un QCM, je sais que la bonne réponse est que l'ensemble des solutions est un cercle (privé d'un point), le souci c'est que je devrai donc arriver à un résultat de la forme (x+a)²+(y+b)²=R, non?
z'=((z*-1)(z+2))/((z*+2)(z+2)) mais ensuite j'ai un quotient z'=(zz*-z-2)/(zz*+2(z+z*)+4)
Je sais aussi que zz*=x²+y² mais je vais partout sauf au bon endroit avec tout ça.
L'exercice est un QCM, je sais que la bonne réponse est que l'ensemble des solutions est un cercle (privé d'un point), le souci c'est que je devrai donc arriver à un résultat de la forme (x+a)²+(y+b)²=R, non?
Modifié en dernier par sazer le 27 Mai 2016, 21:10, modifié 2 fois.
Re: Géométrie complexe
Ah je vois mais si je fais ça je tombe sur une égalité de deux quotients puis le même souci.
(z*z-z+2z*-2)/(z*z+2(z+z*)+4)=(z-1)/(z+2)
Je pense comprendre, le quotient me dérangeai, mais en mettant le calcul dessus sous le même dénominateur je trouverai un quotient nul, et donc numérateur nul, et finalement j'arrivera à un résultat de la forme que tu m'a proposé, merci beaucoup à toi.
(z*z-z+2z*-2)/(z*z+2(z+z*)+4)=(z-1)/(z+2)
Je pense comprendre, le quotient me dérangeai, mais en mettant le calcul dessus sous le même dénominateur je trouverai un quotient nul, et donc numérateur nul, et finalement j'arrivera à un résultat de la forme que tu m'a proposé, merci beaucoup à toi.
Re: Géométrie complexe
Bon ça a été super dur de comprendre ta démarche puisque tu passes ton temps à écrire des trucs vrais pour tout z et tu écris quasiment jamais de truc équivalent à l'équation de départ.
Tu as une équation z' + z'* = 0
Tu veux voir ce qu'elle dit à propos de z donc tu remplaces z' par (z-1)/(z+2) partout, ce qui donne :
(z-1)/(z+2) + (z*-1)/(z*+2) = 0
Après multiplication par (z*+2)(z+2) on obtient (z-1)(z*+2) + (z*-1)(z+2) = 0, etc. (et donc faudra faire gaffe à vérifier ce qui a un sens pour z=-2, le truc de départ n'est pas défini en -2 mais le truc final si)
Tu as une équation z' + z'* = 0
Tu veux voir ce qu'elle dit à propos de z donc tu remplaces z' par (z-1)/(z+2) partout, ce qui donne :
(z-1)/(z+2) + (z*-1)/(z*+2) = 0
Après multiplication par (z*+2)(z+2) on obtient (z-1)(z*+2) + (z*-1)(z+2) = 0, etc. (et donc faudra faire gaffe à vérifier ce qui a un sens pour z=-2, le truc de départ n'est pas défini en -2 mais le truc final si)
Re: Géométrie complexe
Je me suis effectivement très mal exprimé.
Après avoir développer, j'ai obtenu: 2x²+2y²+2x-4=0
Pour avoir mon équation de cercle: (x+(1/2))²+( rac(2)y)²=17/4 ( rac(2) pour racine carrée de deux )
Apparemment le résultat est un cercle privé d'un point mais je ne vois pas lequel et surtout comment le trouver.
Edit:
Le fameux -2, vu que z=/=-2.
Après avoir développer, j'ai obtenu: 2x²+2y²+2x-4=0
Pour avoir mon équation de cercle: (x+(1/2))²+( rac(2)y)²=17/4 ( rac(2) pour racine carrée de deux )
Apparemment le résultat est un cercle privé d'un point mais je ne vois pas lequel et surtout comment le trouver.
Edit:
Le fameux -2, vu que z=/=-2.
Re: Géométrie complexe
Salut !
C'est faux : dans tes "carrés", le coefficient devant "x" et celui devant "y" ne sont pas les mêmes !
2x²+2y²+2x-4 = (x+ 1/2)²+y²=9 donc l'ensemble que tu cherches est le cercle de centre (-1/2,0) et de rayon 3

sazer a écrit:Après avoir développer, j'ai obtenu: 2x²+2y²+2x-4=0
Pour avoir mon équation de cercle: (x+(1/2))²+( rac(2)y)²=17/4 ( rac(2) pour racine carrée de deux )
C'est faux : dans tes "carrés", le coefficient devant "x" et celui devant "y" ne sont pas les mêmes !
2x²+2y²+2x-4 = (x+ 1/2)²+y²=9 donc l'ensemble que tu cherches est le cercle de centre (-1/2,0) et de rayon 3
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Géométrie complexe
salut
un effort dans l'énoncé serait agréable ...
on cherche les complexes z tels que le complexes z' = (z - 1)/(z + 2) soit imaginaire pur ... avec z <> - 2 bien sur ...
en notant z* le conjugué de z on peut alors se passer de sa forme algébrique et utiliser pleinement toute la richesse des complexes et leurs propriétés
z' est imaginaire pur <=> z' - z* <=> (z - 1)(z* + 2) = -(z* - 1)(z + 2) <=> 2zz* + z + z* - 4 = 0 (*)
à partir de là un peu d'astuce et de factorisation de collège nous permet d'écrire :
(*) <=> 4zz* + 2z + 2z* - 8 = 0 <=> (2z + 1)(2z* + 1) = 9 <=> |2z + 1|² = 9 <=> |z + 1/2|² = 9/4
et on reconnaît l'équation du ...

un effort dans l'énoncé serait agréable ...
on cherche les complexes z tels que le complexes z' = (z - 1)/(z + 2) soit imaginaire pur ... avec z <> - 2 bien sur ...
en notant z* le conjugué de z on peut alors se passer de sa forme algébrique et utiliser pleinement toute la richesse des complexes et leurs propriétés
z' est imaginaire pur <=> z' - z* <=> (z - 1)(z* + 2) = -(z* - 1)(z + 2) <=> 2zz* + z + z* - 4 = 0 (*)
à partir de là un peu d'astuce et de factorisation de collège nous permet d'écrire :
(*) <=> 4zz* + 2z + 2z* - 8 = 0 <=> (2z + 1)(2z* + 1) = 9 <=> |2z + 1|² = 9 <=> |z + 1/2|² = 9/4
et on reconnaît l'équation du ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Géométrie complexe
On a
et
donc
donc l'ensemble recherché est le cercle de centre
Re: Géométrie complexe
Tu cherches l'image réciproque de la droite imaginaire pure par l'homographie  , dont l'homographie inverse est
, dont l'homographie inverse est  .
.
C'est le cercle passant par les images de dans l'homographie inverse, c.-à-d. le cercle passant par les points
dans l'homographie inverse, c.-à-d. le cercle passant par les points  ,
,  et
et 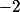 (privé de
(privé de 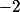 ).
).
C'est le cercle passant par les images de
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
