Bonjour,
Je cherche une méthode simple pour calculer le produit scalaire des vecteurs ->AB et ->AC (je n'ai pas trouvé/beaucoup cherché comment écrire la flèche sur le vecteur) sachant que :
* ABCD est un parallélogramme non croisé
* la distance AB = 3
* la distance AD = 2
* l'angle DÂB mesure 60°
J'ai à ma disposition quasiment le cours de 1ère S (trigonométrie comprise) mais pas le cours appelé "application du produit scalaire" (donc pas de formule des aires, de formule des sinus, d'Al Kashi et compagnie).
J'ai eu l'idée de créer un repère orthonormé direct d'origine A et pour trouver les coordonnées de chaque point puis de trouver le produit scalaire en utilisant les coordonnées des vecteurs ->AB et ->AC.
Mais vu l'exercice (tout début de chapitre) je présume qu'il y a plus simple (en tout cas j'aimerai savoir si on peut l'expliquer avec d'autres notions de cours, plus "simples" que la création d'un repère).
En vous remerciant pour vos réponses.
Produit Scalaire
11 messages
- Page 1 sur 1
Re: Produit Scalaire
Hello,
Tout simplement en appliquant la définition du produit scalaire de deux vecteurs u et v:
u.v = ||u|| * ||v|| * cos(u,v)
Avec (u,v) l'angle entre les deux.
Tout simplement en appliquant la définition du produit scalaire de deux vecteurs u et v:
u.v = ||u|| * ||v|| * cos(u,v)
Avec (u,v) l'angle entre les deux.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Produit Scalaire
Le problème c'est que justement... l'angle entre les 2 vecteurs est inconnue...
On connait la norme du vecteur ->AB et celle du vecteur ->AD (2 "côtés" consécutifs du parallélogramme)
Pas celle du vecteur ->AC ("diagonale").
Or on cherche le produit scalaire entre AB et AC...
il me manque donc comment trouver l'angle BÂC... une propriété du parallélogramme que j'aurai oublié?
On connait la norme du vecteur ->AB et celle du vecteur ->AD (2 "côtés" consécutifs du parallélogramme)
Pas celle du vecteur ->AC ("diagonale").
Or on cherche le produit scalaire entre AB et AC...
il me manque donc comment trouver l'angle BÂC... une propriété du parallélogramme que j'aurai oublié?
Re: Produit Scalaire
bonjour
AB.AC = AB.(AB +BC) = AB ^2 + ( AB .BC) = AB^2 + AB . AD
et comme l'a rappele Lostounet
AB.AD = |AB|*|AD|*cos(DAB)
.......
AB.AC = AB.(AB +BC) = AB ^2 + ( AB .BC) = AB^2 + AB . AD
et comme l'a rappele Lostounet
AB.AD = |AB|*|AD|*cos(DAB)
.......
Re: Produit Scalaire
Tu cherche en gros le produit scalaire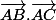
Puisqu'on a un parallélogramme,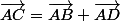 (règle du parallélogramme)
(règle du parallélogramme)
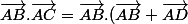 = AB^2 + \vec{AB}. \vec{AD})
Puisqu'on a un parallélogramme,
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Produit Scalaire
Voilà qui est mieux 
Je me disais bien que créer un repère c'était tordu!
Un grand merci !
Je me disais bien que créer un repère c'était tordu!
Un grand merci !
Re: Produit Scalaire
Lostounet a écrit:Hello,
Tout simplement en appliquant la définition du produit scalaire de deux vecteurs u et v:
u.v = ||u|| * ||v|| * cos(u,v)
Avec (u,v) l'angle entre les deux.
Note Lostounet que ce que tu as donné ici, n'est pas(plus) la définition du produit scalaire : en tout cas ce n'est plus celle que l'on trouve dans les manuels scolaires récents (et c'est bien dommage).
Apparemment le programme actuel préfère la version avec les normes au carré des vecteurs ||u||, ||v|| et ||u-v||...
"De mon temps", j'ai aussi appris celle avec les normes et le cosinus...
Enfin bref, merci en tout cas!
A bientôt
Re: Produit Scalaire
Ce que tu avances m'étonne un peu, car je ne date pas d'une époque si lointaine: j'ai fait ma 1ere S post-réforme et c'est bien cette forme là du produit scalaire qui m'a été enseignée en cours?
D'ailleurs de quelle formulation avec les normes veux-tu parler?
Les programmes auraient-ils encore changé?
D'ailleurs de quelle formulation avec les normes veux-tu parler?
Les programmes auraient-ils encore changé?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Produit Scalaire
Salut Lostounet !
Je pense qu'il veut parler de la formule :
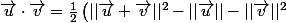)
Je pense qu'il veut parler de la formule :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Produit Scalaire
capitaine nuggets a écrit:Salut Lostounet !
Je pense qu'il veut parler de la formule :
cette formule est toujours intéressante pour introduire le produit scalaire ...
ainsi l'expression
c'est toujours une bonne activité d'approche ...indépendant de toute "définition officielle" du p.s.
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Produit Scalaire
Je parlais effectivement de cette formule :
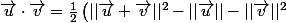) [/quote]
[/quote]
Que je trouve tellement moins efficace que l'autre avec les cosinus (et qui dans la pratique n'est quasiment jamais utilisé dans les exercices données aux élèves).
Merci en tout cas pour vos réponses et désolé pour le long temps de réponse (beaucoup de boulot en ce moment)!
Que je trouve tellement moins efficace que l'autre avec les cosinus (et qui dans la pratique n'est quasiment jamais utilisé dans les exercices données aux élèves).
Merci en tout cas pour vos réponses et désolé pour le long temps de réponse (beaucoup de boulot en ce moment)!
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
