Congruence, système de fonction...

[neil77]

voilà j'ai ce système à résoudre 2x-4y congru 2 modulo6
x+5y congru 2 modulo6

g di ke 2x-4y-2=6k et x+5y-2=6k d'où 2x-4y-2=x+5y-2 donc x = 9y

Ca me parait trop simple pour que ca soit bon... Pouvez vous vérifier? merci

[Zebulon]

Bonjour,
en effet, ce serait trop simple!
En toute généralité, si on a et , alors il existe tels que a-r=kq et b-r=k'q.
Ca ne veut pas dire que k=k'!!!

[neil77]

Oui mais alors je ne sais pas comment faire.

[Zebulon]

On a le système
donc par les combinaisons linéaires et . Il faut maintenant chercher x et y, modulo 6, tels que et .

[neil77]

Pourais-tu m'expliquer autrement je n'ai jamais vu les combinaison linéaire

[Zebulon]

Quand on a un système de deux équations et 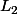, il est équivalent à tout système formé de deux combinaisons linéaires de et 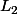(différentes) :
a les mêmes solutions que pour tous (avec quand même la précision : on n'a pas a et b qui sont nuls, ni a' et b' qui sont nuls).


Un exemple serait sûrement le bienvenu :
Soit le système S : .
Alors S a les mêmes solutions que
donc S a les mêmes solutions que
donc S a pour solution .


Ici, on fait pareil!

[neil77]

merci beaucoup pour cette explication

[Zebulon]

Maintenant que vous comprenez pourquoi le système a les mêmes solutions que , il faut chercher x et y deux entiers vérifiant et . On ne peut que les résoudre modulo 6. Voilà comment faire pour y par exemple :
y 0 1 2 3 4 5
-14ymod(6) 0 4 2 0 4 2
(il faut lire ces deux lignes comme un tableau).
car , , , etc...