Bonjour,
J'ai une question sur laquelle je bloque pour étudier une suite.
Soit f(x)= 2/3 (x+ (1/x^2))
J'ai étudié les variations de f, croissante sur -infini,0 puis décroissante sur 0,racine cubique de 2, puis croissante jusqu'à +infini.
Soit la suite x(n+1)= f(xn)
Il faut montrer que la suite xn décroît et converge vers un réel alpha>1, que l'on précisera.
Je pense que ce réel est racine cubique de 2, mais je n'ai aucune idée d ecomment le démontrer, j'ai pensé à la récurrence pour montrer que la suite était décroissante mais il y a deux termes en xn donc je n'y arrive pas de cette manière..
Suites
6 messages
- Page 1 sur 1
Re: Suites
Hey,
On te donne pas x0?
Effectivement en résolvant f(x)=x, on tombe sur racine cubique de 2.
On te donne pas x0?
Effectivement en résolvant f(x)=x, on tombe sur racine cubique de 2.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Suites
salut
posons
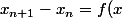 - x = \dfrac 2 3(x + \dfrac 1 {x^2}) - x = - \dfrac 1 3 (x - \dfrac 2 {x^2}) = -\dfrac 1 {3x^2}(x^3 - 2) = -\dfrac 1 {3x^2}(x - r)(x^2 + xr + r^2))
1/3x^2 et x^2 + rx + r^2 sont positifs
si x_n > r alors par récurrence ::
1/ x_{n + 1} > r
2/ (x_n) est décroissante
x_0 = 1/2 ne vérifie pas 1/ donc il faut initialiser au bon rang
....
posons
1/3x^2 et x^2 + rx + r^2 sont positifs
si x_n > r alors par récurrence ::
1/ x_{n + 1} > r
2/ (x_n) est décroissante
x_0 = 1/2 ne vérifie pas 1/ donc il faut initialiser au bon rang
....
Modifié en dernier par zygomatique le 30 Mar 2016, 19:42, modifié 1 fois.
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Suites
Bonjour,
Essaie de tracer la fonction et la suite (en utilisant la droite d'equation y=x), ça te permettra peut être de mieux voir pourquoi il faut passer par le point invariant de la fonction comme l'a dit Lostounet
Essaie de tracer la fonction et la suite (en utilisant la droite d'equation y=x), ça te permettra peut être de mieux voir pourquoi il faut passer par le point invariant de la fonction comme l'a dit Lostounet
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
