Comprend pas trop
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Darcky
- Messages: 5
- Enregistré le: 03 Oct 2006, 20:03
-
 par Darcky » 03 Oct 2006, 20:09
par Darcky » 03 Oct 2006, 20:09
voila ben j'ai un DM pour lundi et je mis met maintenant mais le premier exo me pose des problemes, je suis en Terminale S .
ennoncé :
soit f une fonction continue et definie sur [0;1] et à valeur dans l'intervalle [0;1]. Demontrer que f admet ( au moins ) un point fixe dans [0;1]
voila, l'ennoncer se resume a ca, je n'ai pas la fonction et je voi pa tellement sur koi il fo que je parte, ni quoi faire pour arriver a la bonne réponse.
merci a ceux qui peuvent me filer un coup de main
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 03 Oct 2006, 20:14
par Imod » 03 Oct 2006, 20:14
Essaie de considérer g(x)=x-f(x) .
Imod
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Oct 2006, 20:18
par nada-top » 03 Oct 2006, 20:18
bonsoir ,
démontrer que f admet au moins un point fixe , revient à démontrer qu'il existe
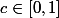
t.q f(c) = c .
donc il suffit d'étudier la fonction définie par: g(x) = f(x)-x et appliquer TVI .
bon courage .
-
Darcky
- Messages: 5
- Enregistré le: 03 Oct 2006, 20:03
-
 par Darcky » 03 Oct 2006, 20:19
par Darcky » 03 Oct 2006, 20:19
je suis d'accord mais a vrai dir je voi pa trop que faire avec g(x)=x-f(x) je doit demontrer que f a des point fixe dans [0;1] mais ajouter une autre fonction inconnu ne va pas plutot me compliquer les choses?
-
Darcky
- Messages: 5
- Enregistré le: 03 Oct 2006, 20:03
-
 par Darcky » 03 Oct 2006, 20:20
par Darcky » 03 Oct 2006, 20:20
ah je voi mieix maintenant. merci beacoup je vais essayer de travailler avec ceci. mais pourais-tu m'expliquer pourquoi on prend g(x)=f(x)-x ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:22
par Zebulon » 03 Oct 2006, 20:22
Bonsoir,
quels sont les signes de g(0) et g(1), avec g comme introduite par nada-top?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Oct 2006, 20:29
par nada-top » 03 Oct 2006, 20:29
merci beacoup je vais essayer de travailler avec ceci. mais pourais-tu m'expliquer pourquoi on prend g(x)=f(x)-x ?
rappel : si
)
est continue sur [a,b] et
.f(b) < 0)
, alors selon TVI : il existe
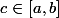
t.q :
 = 0)
donc maitenant si tu démontre qu'il existe
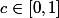
t.q g(c) = 0 , tu auras
-c=0)
soit
 = c)
.cqfd
-
Darcky
- Messages: 5
- Enregistré le: 03 Oct 2006, 20:03
-
 par Darcky » 03 Oct 2006, 20:30
par Darcky » 03 Oct 2006, 20:30
donc si je comprend bien il faut que je fasse g(0)=f(0)-0 soirt g(0)=f(0) et g(1)=f(1)-1 , mais je ne voi pas ce que je peu en deduir.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:35
par Zebulon » 03 Oct 2006, 20:35
Soit

, g(x)=f(x)-x.
On sait que f est à valeurs dans [0,1] ce qui s'écrit encore :
pour tout
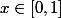
,
}\leq1)
. Déduisez-en le signe de g(0) et de g(1).
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Oct 2006, 20:39
par nada-top » 03 Oct 2006, 20:39
f une fonction continue et definie sur [0;1] et à valeur dans l'intervalle [0;1].
c-à-d que f est définie de
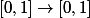
i.e
 \leq)
et
 \leq 1)
...donc?
-
Darcky
- Messages: 5
- Enregistré le: 03 Oct 2006, 20:03
-
 par Darcky » 03 Oct 2006, 20:54
par Darcky » 03 Oct 2006, 20:54
donc j'arrive ces encadrements :
0 < g(0) < 1 et -1 < g(1) < 0
de la je dis que sur [0;1] g(x) et strictement decroissante et continue, qu'il existe bien c e [0;1] tq g(c)=0 et je conclu
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Oct 2006, 21:03
par nada-top » 03 Oct 2006, 21:03
de la je dis que sur [0;1] g(x) et strictement decroissante et continue, qu'il existe bien c e [0;1] tq g(c)=0
d'abord g(x) est un nombre et g c'est la fonction .
ensuite on cheche pas à démontrer la stricte monotonie de g , mais juste
.g(1)\leq 0)
.
donc moi je dirais : g est continue sur [0,1] et on a
.g(1) \leq 0)
, donc

:
 = 0)
.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 03 Oct 2006, 21:21
par nada-top » 03 Oct 2006, 21:21
on cheche à démontrer la stricte monotonie , si on veut prouver l'unicité d'un tel c (il existe
un unique c ..)... mais maintenant il suffit de prouver l'existence de c (il existe
au moins un c ..) ...dans ce cas on prouve que
g(1) \leq 0)
(+la continuité).
ok??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
