Suites adjacentes

[pandad]

Bonsoir!

Soient (un) et (vn) 2 suites definies par u0=2 , un+1=(un+vn)/2 et v0=1 , vn+1=radical(un*vn) .
1 ) Montrer que vn<un et puis que un+1-vn+1<(un-vn)/2 .

J'ai montre par recurrence que vn<un , mais je n'arrive pas a resoudre la deuxieme inegalite .

2)Montrer que les suites sont adjacentes.
Donc j'ai trouve un croissante . Pour vn je n'arrive pas trouver la monotonie .
Et pour lim(vn -un) je ne veux pas comment resoudre

[Ben314]

Salut,
Montrer que revient à montrer que avec .

Pour montrer qu'une telle inégalité est vrai, il faut évidement enlever la méchante racine qui apparait là dedans pour se ramener à un gentil polynôme. Deux solutions :
1) Isoler la racine et élever les deux termes au carré (en faisant attention aux signes...)
2) Poser et .

Le fait que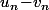 tende vers 0 découle immédiatement de la relation qui implique, par une récurrence "immédiate" que, pour tout n, on a

[pandad]

D'accord, j'ai compris . Merci beaucoup