Comme

,
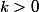
et
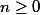
L'étude de la fonction obtenue par M. Zygomatique et qui est :
 = (1 - r) k^{n + 1} + r k^n - 1 = 0)
, donne :
Pour
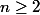
:
On a
 = - 1)
et
 = + \infty)
.
On a aussi
 = (n + 1) (1 - r) k^n + n r k^{n - 1} = k^{n - 1} ((n + 1) (1 - r) k + n r))
, donc pour
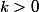
on a
 > 0)
, donc f est strictement croissante pour
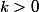
, et comme elle est continue sur

donc c'est une bijection de

sur

, et donc elle s'annule pour une unique valeur de k.
On a une racine évidente de
 = (1 - r) k^{n + 1} + r k^n - 1 = 0)
qui est k = 1 et qui est la seule racine de l'équation donnée.
Pour n = 0 , on a (1 - r) k + r - 1 = 0 ce qui donne

.
Pour n = 1 , on a
 k^2 + r k - 1 = 0)
, équation qui a pour discriminant
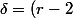}^2)
et qui donne k = 1.
Donc
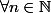
on a pour l'équation donnée une unique racine qui est
k = 1 , ceci sous toutes les réserves logiques et mathématiques.

 particulier il est impossible de résoudre exactement cette équation ....
particulier il est impossible de résoudre exactement cette équation ....