Matrice I: Propriété
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 20 Jan 2016, 13:45
par biss » 20 Jan 2016, 13:45
Bonjour, n'ayant pas trop de notion sur les matrices alors je vous demande si vous pouvez me corrigé sur cet exercice
On nous donne une matrice A
1)calculé
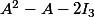
j'ai trouvé 0
2) montrer que A est inversible et en déduire A^{-1}.
Donc on a
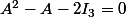
=2I_3)
(\frac{1}{2}\frac{1}{I_3}=I_3)
(0.5)I_3=I_3)
=I_3)
Donc A est inversible et son inverse est

.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 20 Jan 2016, 13:49
par aymanemaysae » 20 Jan 2016, 13:49
Pour moi c'est juste.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Jan 2016, 14:01
par Carpate » 20 Jan 2016, 14:01
aymanemaysae a écrit:Pour moi c'est juste.
Mais ça pourrait être plus direct
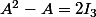
A-A^{-1}A=2A^{-1})
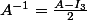
Modifié en dernier par
Carpate le 20 Jan 2016, 14:06, modifié 2 fois.
 par cauchy-schwartz » 20 Jan 2016, 14:01
par cauchy-schwartz » 20 Jan 2016, 14:01
Slt,
Je crois qu'il est important de démontrer que A est inversible <=> det A<>0 ou autre propriété avant d'entamer le calcul. Si l'inverse n'existe pas, on ne peut pas l'utiliser.
CS
Modifié en dernier par
cauchy-schwartz le 20 Jan 2016, 14:04, modifié 1 fois.
-
Robot
 par Robot » 20 Jan 2016, 14:12
par Robot » 20 Jan 2016, 14:12
Bien sûr que non, CS.
La démarche est complète, on montre que A est inversible en exhibant explicitement (en fonction de A) un inverse.
Question de goût, j'ai horreur du 0.5 pour écrire 1/2, parce qu'il laisse penser qu'on travaille en flottants.
Le

ne me plait pas du tout non plus. On n'écrit jamais de matrice au dénominateur !
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 20 Jan 2016, 16:47
par biss » 20 Jan 2016, 16:47
Je vois.
Merci j'ai compris.
 par cauchy-schwartz » 20 Jan 2016, 18:51
par cauchy-schwartz » 20 Jan 2016, 18:51
Pour biss, ça va; c'est pour Carpate qui utilise l'inverse. Avant de l'utiliser, il me semblait qu'il fallait le prouver.
CS
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Jan 2016, 19:18
par Carpate » 20 Jan 2016, 19:18
cauchy-schwartz a écrit:Pour biss, ça va; c'est pour Carpate qui utilise l'inverse. Avant de l'utiliser, il me semblait qu'il fallait le prouver.
CS
En l'absence de l'Arlésienne : la matrice que biss a choisi de nous cacher, il était difficile de montrer directement qu'elle est inversible.
Tout ce qu'on peut déduire c'est qu'elle est diagonalisable car de valeurs propres distinctes : -1 et 2 ...

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 20 Jan 2016, 21:00
par alm » 20 Jan 2016, 21:00
A vrai dire, un élément

d'un anneau
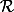
est inversible s'il existe

tel que

.
Si c'est cette définition qui est adoptée dans ton cours il ne faut pas négliger de signaler que

où
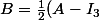)
.
Si cependant le cours donne la proposition: une matrice carrée est inversible si et seulement si elle est inversible à droite ou à gauche, auquel cas les trois inverses sont égaux alors ce qui est écrit au premier topic suffit comme preuve.
Pour profiter de cela on peut justement faire l'exo:
Soit
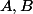
deux matrices carrées (réelles) de taille

tel que
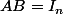
, démontrer que
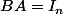
.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 21 Jan 2016, 14:59
par aymanemaysae » 21 Jan 2016, 14:59
On a
 = 1 \rightarrow \det(A) \det(B) = 1 \rightarrow \det(A) \ne 0)
et
 \ne 0)

A et B sont inversibles.
On a
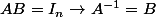
et
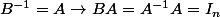
.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 21 Jan 2016, 16:36
par Carpate » 21 Jan 2016, 16:36
On peut considérer le polynôme minimal de l'endomorphisme que représente A dans la base canonique de

:

dont les racines -1 et 2 sont
différentes de 0 ce qui est une condition nécessaire et suffisante d'inversibilité de A
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 21 Jan 2016, 20:43
par biss » 21 Jan 2016, 20:43
aymanemaysae a écrit:On a
 = 1 \rightarrow \det(A) \det(B) = 1 \rightarrow \det(A) \ne 0)
et
 \ne 0)

A et B sont inversibles.
On a
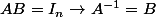
et
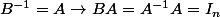
.
Je prend note. Merci
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 21 Jan 2016, 20:44
par biss » 21 Jan 2016, 20:44
Carpate a écrit:On peut considérer le polynôme minimal de l'endomorphisme que représente A dans la base canonique de

:

dont les racines -1 et 2 sont
différentes de 0 ce qui est une condition nécessaire et suffisante d'inversibilité de A
Peut être me manque encore certains notion pour comprendre le différent de 0 alors c'est inversible.
Modifié en dernier par
biss le 21 Jan 2016, 20:48, modifié 1 fois.
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 21 Jan 2016, 20:46
par biss » 21 Jan 2016, 20:46
alm a écrit:A vrai dire, un élément

d'un anneau
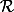
est inversible s'il existe

tel que

.
Si c'est cette définition qui est adoptée dans ton cours il ne faut pas négliger de signaler que

où
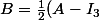)
.
Si cependant le cours donne la proposition: une matrice carrée est inversible si et seulement si elle est inversible à droite ou à gauche, auquel cas les trois inverses sont égaux alors ce qui est écrit au premier topic suffit comme preuve.
Pour profiter de cela on peut justement faire l'exo:
Soit
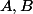
deux matrices carrées (réelles) de taille

tel que
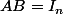
, démontrer que
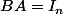
.
Je prend note pour mes futures exercices.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 22 Jan 2016, 10:44
par Carpate » 22 Jan 2016, 10:44
Biss
Pourrais-tu nous donner les 9 coefficients de cette matrice ?
Merci
-
Robot
 par Robot » 22 Jan 2016, 11:03
par Robot » 22 Jan 2016, 11:03
A quoi cela servirait-il ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 22 Jan 2016, 11:26
par Carpate » 22 Jan 2016, 11:26
Je voulais calculer les valeurs propres
-
Robot
 par Robot » 22 Jan 2016, 11:32
par Robot » 22 Jan 2016, 11:32
Bah, on sait qu'elles sont parmi les racines de

. A quoi ça nous avancerait de plus pour le problème de l'inversibilité de

?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 22 Jan 2016, 14:48
par Carpate » 22 Jan 2016, 14:48
A avoir la 3ème VP
Simple curiosité ...
-
Robot
 par Robot » 22 Jan 2016, 15:15
par Robot » 22 Jan 2016, 15:15
Il n'y a pas de 3e valeur propre (distincte). Il n'y a même peut-être qu'une seule valeur propre, mais ça ne change rien pour l'inversibilité, ni rien sur l'expression de l'inverse comme polynôme en A.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
et
A et B sont inversibles.
et
.
:
dont les racines -1 et 2 sont différentes de 0 ce qui est une condition nécessaire et suffisante d'inversibilité de A
d'un anneau
est inversible s'il existe
tel que
.
où
.
deux matrices carrées (réelles) de taille
tel que
, démontrer que
.