Suites

par **sidone25** » 22 Déc 2015, 15:51

Bonjour j'ai un sujet de DM me voici :
On considère me suite Un définie par Uo = 1,
Un+1=1+ 1/(Un + 1) avec le 1 pas en indice dans la fraction.
1)a)Calculer U1... U4 ainsi que U1^2 - 2 , U2^2 - 2 jusqu'à U4
b) que pouvez vous déduire du sens DE variation?
c) montrer par récurrence
que 1<= Un<= 3/2
2)A) on définit la suite par Vn=(Un-racine de 2)/(Un+racine de 2)
Montrer que Vn est géométrique de raison q=(1-racine DE 2)/(1+racine de 2)
2b) en déduire l'expression de Vn en fonction de n et sa limite.
3a) montrer que pour tout n Un=racine de 2 x (1+Vn)/(1-Vn)
Tout ça est déjà fait mais je bloque sur la dernière question qui est :
B) en déduire que racine de 2 -Un= 2q^n/(1+q^n)
Voila si vous pouviez m'aider pour cette dernière je vous en serait très reconnaissant.

par **biss** » 22 Déc 2015, 17:01

sidone25 a écrit:Bonjour j'ai un sujet de DM me voici :
On considère me suite Un définie par Uo = 1,
Un+1=1+ 1/(Un + 1) avec le 1 pas en indice dans la fraction.
1)a)Calculer U1... U4 ainsi que U1^2 - 2 , U2^2 - 2 jusqu'à U4
b) que pouvez vous déduire du sens DE variation?
c) montrer par récurrence
que 1<= Un<= 3/2
2)A) on définit la suite par Vn=(Un-racine de 2)/(Un+racine de 2)
Montrer que Vn est géométrique de raison q=(1-racine DE 2)/(1+racine de 2)
2b) en déduire l'expression de Vn en fonction de n et sa limite.
3a) montrer que pour tout n Un=racine de 2 x (1+Vn)/(1-Vn)
Tout ça est déjà fait mais je bloque sur la dernière question qui est :
B) en déduire que racine de 2 -Un= 2q^n/(1+q^n)
Voila si vous pouviez m'aider pour cette dernière je vous en serait très reconnaissant.

Tu as besoin d'aide juste pour la dernière question ? Où tu en ai ?

par **sidone25** » 22 Déc 2015, 17:05

biss a écrit:Tu as besoin d'aide juste pour la dernière question ? Où tu en ai ?

J'ai fait toutes les questions sauf la dernière !

par **biss** » 22 Déc 2015, 17:12

sidone25 a écrit:J'ai fait toutes les questions sauf la dernière !

Tu sais que Vn=voq^n
Dans l'expression Un=...
Tu as essayé de remplacer dans Un, Vn par son expression que j'ai dis. Puis mettre 2-Un=? Et arrangée un peu ?

par **sidone25** » 22 Déc 2015, 17:15

biss a écrit:Tu sais que Vn=voq^n
Dans l'expression Un=...
Tu as essayé de remplacer dans Un, Vn par son expression que j'ai dis. Puis mettre 2-Un=?

Oui c'est ce que j'ai essayé de faire mais je me retrouve avec des choses qui n'ont rien à voir... J'arrive pas à retrouver q^n dans l'expression finale...

par **biss** » 22 Déc 2015, 18:03

sidone25 a écrit:Bonjour j'ai un sujet de DM me voici :
On considère me suite Un définie par Uo = 1,
Un+1=1+ 1/(Un + 1) avec le 1 pas en indice dans la fraction.
1)a)Calculer U1... U4 ainsi que U1^2 - 2 , U2^2 - 2 jusqu'à U4
b) que pouvez vous déduire du sens DE variation?
c) montrer par récurrence
que 1<= Un<= 3/2
2)A) on définit la suite par Vn=(Un-racine de 2)/(Un+racine de 2)
Montrer que Vn est géométrique de raison q=(1-racine DE 2)/(1+racine de 2)
2b) en déduire l'expression de Vn en fonction de n et sa limite.
3a) montrer que pour tout n Un=racine de 2 x (1+Vn)/(1-Vn)
Tout ça est déjà fait mais je bloque sur la dernière question qui est :
B) en déduire que racine de 2 -Un= 2q^n/(1+q^n)
Voila si vous pouviez m'aider pour cette dernière je vous en serait très reconnaissant.

La formule de Un doit comporte des erreur puisque U1=3/2 est différent de U1=(-2q)/(1+q)+2 (sauf si je me suis trompé mais tu pourra essayé aussi)
Sinon à part l'erreur tu peux aussi tenté (si U1=U1)
Comme on a

alors.

Tu vas essayé de retrouver cet expression en partant de

par **sidone25** » 22 Déc 2015, 18:32

biss a écrit:La formule de Un doit comporte des erreur puisque U1=3/2 est différent de U1=(-2q)/(1+q)+2 (sauf si je me suis trompé mais tu pourra essayé aussi)
Sinon à part l'erreur tu peux aussi tenté (si U1=U1)
Comme on a alors.
Tu vas essayé de retrouver cet expression en partant de

Ah oui vous avez effectivement raison on vient de me dire que l'énoncé à un problème et que finalement la question 3b serait : écrire racine de 2 - Un en fonction de q^n.
Est ce que ce changement d'enoncé vous inspire quelque chose..? Je dois remplacer Vn dans la formule de Un puis trouver quelque chose en fonction de q^n ?

par **Ben314** » 22 Déc 2015, 19:08

Salut,
Partant de

tu peut en déduire la valeur de Un en fonction de Vn et comme tu connait la valeur de Vn en fonction de n, ça te donnera Un en fonction de n.

par **sidone25** » 22 Déc 2015, 19:14

Ben314 a écrit:Salut,
Partant de tu peut en déduire la valeur de Un en fonction de Vn et comme tu connait la valeur de Vn en fonction de n, ça te donnera Un en fonction de n.

Bonsoir, c'est ce que je tente de faire mais je pense que j'ai un problème calculatoire étant donné que j'arrive à un résultat incohérent...

par **Ben314** » 22 Déc 2015, 19:16

Tu obtient quoi comme résultat ?

par **sidone25** » 22 Déc 2015, 19:26

Ben314 a écrit:Tu obtient quoi comme résultat ?

Deja pour Vn=[(1-racine de 2)/(1+racine de 2)]^(n+1) c'est bien cela ?

Ensuite en développant tout j'obtiens racine de 2[(2*(1-racine de 2^n+1))/(-2*(1+racine de 2^n+1)]
Et je bloque
C'est totalement incohérent

par **Ben314** » 22 Déc 2015, 20:03

A mon avis, déjà, il vaudrait mieux garder la lettre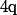

plutôt que de recopier à oute les lignes la fraction compliquée

.
Ensuite, comme

est géométrique de raison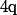

on a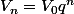

pour tout n, et comme

donc on a effectivement

pour tout n.
Mais, personne ne te demande de développer

et en plus, si on te le demandais, ça ne ferait pas du tout ce que tu dit vu que

(déjà, avec n=2 il est bien connu que (A+B)²=A²+2AB+B² et pas A²+B² !!!). De plus, le résultat qu'on te demande d'établir contient la lettre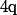

donc tu le garde tel quel.

Bilan : c'est bon tu as Vn en fonction de n (et de q, mais ça on s'en fout).
As-tu la formule donnant Un en fonction de Vn ?
Si oui, ben tu remplace Vn par

dans cette formule et c'est fini...

par **sidone25** » 22 Déc 2015, 20:27

Ben314 a écrit:A mon avis, déjà, il vaudrait mieux garder la lettre plutôt que de recopier à oute les lignes la fraction compliquée .
Ensuite, comme est géométrique de raison on a pour tout n, et comme donc on a effectivement pour tout n.
Mais, personne ne te demande de développer et en plus, si on te le demandais, ça ne ferait pas du tout ce que tu dit vu que (déjà, avec n=2 il est bien connu que (A+B)²=A²+2AB+B² et pas A²+B² !!!). De plus, le résultat qu'on te demande d'établir contient la lettre donc tu le garde tel quel.

Bilan : c'est bon tu as Vn en fonction de n (et de q, mais ça on s'en fout).
As-tu la formule donnant Un en fonction de Vn ?
Si oui, ben tu remplace Vn par dans cette formule et c'est fini...

Ahhhh oui c'est donc aussi simple que ça. J'ai bien l'expression de Un en fonction de Vn, du coup c'est un jeu d'enfant! Merci beaucoup pour vos explications très claires, je vais donc enfin pouvoir finir ce DM. Merci encore, bonne soirée à vous !

par **Ben314** » 22 Déc 2015, 21:28

Normalement (i.e. si je me suis pas gourré...) tu devrait obtenir

et il y a une petite erreur dans l'énoncé de départ...

par **sidone25** » 22 Déc 2015, 23:34

Ben314 a écrit:Normalement (i.e. si je me suis pas gourré...) tu devrait obtenir
et il y a une petite erreur dans l'énoncé de départ...

Merci d'avoir pris le temps de m'aider, je vais essayer de faire ça demain et je vous redirai si je trouve bien la meme chose que vous !

par **sidone25** » 04 Jan 2016, 21:31

sidone25 a écrit:Merci d'avoir pris le temps de m'aider, je vais essayer de faire ça demain et je vous redirai si je trouve bien la meme chose que vous !

Bonjour je ne sais pas si vous êtes encore disponible pour m'aider meme si ce sujet date s'il y a longtemps... En fait je ne comprends pas comment arriver à racinede2-Un ?

par **sidone25** » 05 Jan 2016, 08:44

Ben314 a écrit:Normalement (i.e. si je me suis pas gourré...) tu devrait obtenir
et il y a une petite erreur dans l'énoncé de départ...

Bonjour je ne sais pas si vous êtes encore disponible pour m'aider meme si ce sujet date s'il y a longtemps... En fait je ne comprends pas comment arriver à racinede2-Un ?

Suites

Suites

Qui est en ligne