Maths term

par **mathilde98** » 21 Déc 2015, 23:05

En fait je pense que je ne comprends pas pourquoi
F(n+1)x est superieur à Fn(x)...
Pourtant je le lis et le relis mais...

par **mathilde98** » 21 Déc 2015, 23:06

Après je comprends tout ce que vous écrivez mais je bloque à ce niveau la..

par **Ben314** » 22 Déc 2015, 00:11

Y'a qu'à changer de méthode, on verra si tu comprend mieux...
Pour savoir si

est plus grand ou plus petit que

(pour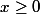

) on étudie le signe de la différence entre les deux.

Comme

il reste à étudier le signe de

.

est du signe de

donc négatif si

et positif si

.
La fonction g est donc décroissante sur [0,a] puis croissante sur [a,+oo[ ce qui signifie qu'elle a un minimum en x=a.
Or

car

pour tout x positif.

A noter que c'est bien plus long que la petite disjonction de cas utilisé dans le post ci dessus....

par **mathilde98** » 22 Déc 2015, 08:34

Ah d accord je comprends tout maintenant!! Merci beaucoup pour votre patience!;)
Et du coup quand on a fait ca on remplace x par Un

Ce qui après permet de montrer que U(n+1) est inférieur à Un lui meme inférieur à 1/n

Donc la suite Un est décroissante et bornée donc elle converge

Et sa limite est 0 c est ca?

par **mathilde98** » 22 Déc 2015, 10:18

mais d'ailleurs comment on sait que a est compris entre 0 et 1 pour g?

par **mathilde98** » 22 Déc 2015, 10:22

ah mais ca c'est parce qu'on a réduit l'intervalle a [0;1]?

mais j'ai le droit de faire ca? de m'occuper que de cet intervalle?

par **Ben314** » 22 Déc 2015, 15:49

Si tu parle du

du post ci dessus, il vaut

donc il est plus petit que 1. Je l'ai appelé

uniquement parce que j'avais la flemme de recopier 4 fois la formule

...

Sinon, je t'inciterais bien à faire un dessin avec les courbes des fonctions f1,f2,f3 et f4 histoire de bien comprendre le fait que, par exemple, comme f3 et f4 sont toutes les eux croissantes et que la courbe de f4 est au dessus de celle de f3, ça veut dire que la courbe de f4 coupe l'axe des x avant celle de f3 donc que U4<U3.

par **mathilde98** » 22 Déc 2015, 16:50

Ben314 a écrit:Si tu parle du du post ci dessus, il vaut [T EX]4$1-\frac{1}{n}[/TEX] donc il est plus petit que 1. Je l'ai appelé uniquement parce que j'avais la flemme de recopier 4 fois la formule ...

Sinon, je t'inciterais bien à faire un dessin avec les courbes des fonctions f1,f2,f3 et f4 histoire de bien comprendre le fait que, par exemple, comme f3 et f4 sont toutes les eux croissantes et que la courbe de f4 est au dessus de celle de f3, ça veut dire que la courbe de f4 coupe l'axe des x avant celle de f3 donc que U4<U3.

ah oui d'accord pour a!

mais du coup ce que je vous ai écrit pour la suite de la question est ce que c'est correct?

et oui d'accord je vais essayer de faire les courbes!

par **Ben314** » 22 Déc 2015, 17:02

Oui, la limite, c'est bien 0 et, en fait, on n'a pas besoin de la décroissance pour le montrer : le fait que Un soit entre 0 et 1/n suffit grâce au théorème des gendarmes.

par **mathilde98** » 22 Déc 2015, 23:12

Ben314 a écrit:Oui, la limite, c'est bien 0 et, en fait, on n'a pas besoin de la décroissance pour le montrer : le fait que Un soit entre 0 et 1/n suffit grâce au théorème des gendarmes.

oui mais comme je dois étudier la monotonie!!

en tous cas merci beaucoup beaucoup pour votre patience!!! vous m'avez soulagé d'un poids!

Maths term

Qui est en ligne