Maths term

[mathilde98]

Bonjour à tous! ;)
Voila j ai un exercice de maths que je n arrive pas du tout à faire alors je voulais essayer de trouver un petit peu d aide si c est posisble;)

Voila on a une équation
Pour tout n supérieur ou égal à 1

x^(n) + xn -1 = 0

1) montrer que l équation admet une unique solution Un

Alors j ai posé une fonction fn et je l ai dervie et ca me donnait
nx^(n-1) + n
Puis j ai factorie par n
J ai donc obtenu
n(x^(n-1) +1)

J ai ensuite montre que ce qu il y a dans la parenthèse est forcément positif pour n supérieur à 1
Donc ma fonction est strictement croissante sur moins l infini et plus l infini
Mais après je veux utiliser le corrollaire du théorème des valeurs intermédiaires sauf que je n arrive pas a Montrer que 0 appartient à a l intervalle des limite de moins l Infini et plus l infini car je n arrive pas a calculer les limites...

2) étudier la monotonie de la suite Un et montrer qu elle converge et calculer la limite
Et la j ai dit que
Fn(Un) =0
F(n+1)(U(n+1))=0
Et donc j ai voulu calculer
Fn(U(n+1))
Mais la je bloque je n'arrive pas à étudier ses variations et Montrer qu elle est bornée..


Merci d avance;)

[Ben314]

Salut,

J ai donc obtenu
n(x^(n-1) +1)
J ai ensuite montre que ce qu il y a dans la parenthèse est forcément positif pour n supérieur à 1

Ca vaut combien lorsque et ?

[mathilde98]

Salut,Ca vaut combien lorsque et ?

Ah oui mince... Mais du coup comment je fais pour montrer le signe car elle est du coup positive quand n est pair pour tous les x
Elle est négative quand x est négative et n impair...

[biss]

Bonjour à tous!
Voila j ai un exercice de maths que je n arrive pas du tout à faire alors je voulais essayer de trouver un petit peu d aide si c est posisble;)

Voila on a une équation
Pour tout n supérieur ou égal à 1

x^(n) + xn -1 = 0

1) montrer que l équation admet une unique solution Un

Alors j ai posé une fonction fn et je l ai dervie et ca me donnait
nx^(n-1) + n
Puis j ai factorie par n
J ai donc obtenu
n(x^(n-1) +1)

J ai ensuite montre que ce qu il y a dans la parenthèse est forcément positif pour n supérieur à 1
Donc ma fonction est strictement croissante sur moins l infini et plus l infini
Mais après je veux utiliser le corrollaire du théorème des valeurs intermédiaires sauf que je n arrive pas a Montrer que 0 appartient à a l intervalle des limite de moins l Infini et plus l infini car je n arrive pas a calculer les limites...

2) étudier la monotonie de la suite Un et montrer qu elle converge et calculer la limite
Et la j ai dit que
Fn(Un) =0
F(n+1)(U(n+1))=0
Et donc j ai voulu calculer
Fn(U(n+1))
Mais la je bloque je n'arrive pas à étudier ses variations et Montrer qu elle est bornée..


Merci d avance;)

La limite en +infini=+infini ( ça tu as pu le faire )
Mais je ne pense pas qu'il faut calculé la limite en -infini car il doit avoir un intervalle de valeurs pour x qui doit certainement ressemblé à ça x;)0 ( un truc comme ça ) car sinon pour x=-4 et n=4 alors f' est nnégative

[mathilde98]

Oui j avais trouvé la limite en plus l infini!;)
Mais c est pour ça que je bloque en fait car quand x est négatif la fonction la dérivée est négative si n est impair sinon elle positive

Le truc c est que je ne vois pas comment réduire l intervalle car on ne me précise rien... Donc normalement Moins l infini est pris en compte

[mathilde98]

La limite en +infini=+infini ( ça tu as pu le faire )
Mais je ne pense pas qu'il faut calculé la limite en -infini car il doit avoir un intervalle de valeurs pour x qui doit certainement ressemblé à ça x;)0 ( un truc comme ça ) car sinon pour x=-4 et n=4 alors f' est nnégative

T

Mais sinon on peut pas dire que la suite est strictement croissante sur 0 plus l infini et comme avant 0 c est très fluctuant in ne le prend pas en compte?

Le truc c est que fn(0)=0 donc le corrollaire du tvi marche pas la

[Ben314]

Bon, déjà, (et pas 0) et le problème n'est pas d'inventer des contrainte comme bon nous semble, mais de lire correctement l'énoncé.
Donc l'énoncé exact, c'est :
1) Montrer que pour tout entier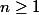 l'équation admet une unique solution réelle.
ou bien
2) Montrer que pour tout entier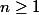 l'équation admet une unique solution positive.

Dans le cas 1), il y a une errer d'énoncé (vu que le truc à montrer est faux) et dans le cas 2) tu ne doit étudier la fonction fn que sur [0,+oo[

[biss]

Tu as raison Ben
@:matilde[de plus

[mathilde98]

Bon, déjà, (et pas 0) et le problème n'est pas d'inventer des contrainte comme bon nous semble, mais de lire correctement l'énoncé.
Donc l'énoncé exact, c'est :
1) Montrer que pour tout entier l'équation admet une unique solution réelle.
ou bien
2) Montrer que pour tout entier l'équation admet une unique solution positive.

Dans le cas 1), il y a une errer d'énoncé (vu que le truc à montrer est faux) et dans le cas 2) tu ne doit étudier la fonction fn que sur [0,+oo[

Ah oui vous avez raison comme la solution est positive alors on peut réduire l ensemble de def a o plus l infini!! Et le corrollaire du tvi fonctionne du coup!;)

Super merci beaucoup!!
mais du coup pour la question 2 je ne vois pas comment faire tout de même...

[Ben314]

Donc tu confirme que l'énoncé, c'est bien "montrer que l'équation a une solution positive" ?

Sinon, pour la 2), je commencerais par comparer les fonctions et 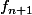: le calcul n'est pas immédiat, mais tu devrait arriver à montrer que pour tout 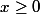on a .
Ensuite, la grosse astuce, c'est d'appliquer cette inégalité à (ou a , comme tu veut...)

[mathilde98]

Donc tu confirme que l'énoncé, c'est bien "montrer que l'équation a une solution positive" ?

Sinon, pour la 2), je commencerais par comparer les fonctions et : le calcul n'est pas immédiat, mais tu devrait arriver à montrer que pour tout on a .
Ensuite, la grosse astuce, c'est d'appliquer cette inégalité à (ou a , comme tu veut...)

oui l'énoncé parlait d'une solution positive!


oui mais en fait j'ai essayé de faire ca sauf que je me retouve avec
fn(x)= x^(n) + nx - 1
f(n+1) (x)= x^(n+1) +nx+ x -1

donc en fait après je remplace par Un et comme fn(Un) = 0 alors
Un^(n) + nUn -1 =0
d'ou
nUn-1 = - Un^(n)

je remplace après cette égalité
f(n+1)(Un)= Un^(n+1) -Un^(n) + Un

et la comment je trouve les variations?

[Ben314]

Il faut commencer par montrer que pour tout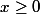
c'est à dire montrer que
soit encore
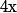Si , c'est vrai et, si en divisant par il faut montrer que
Là, deux cas se présentent :
Soit )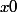

Ensuite, tu applique cette inégalité avec : et comme par définition de ça te dit que
Donc la fonction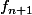 est négative en et positive en 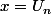ce qui signifie qu'elle s'annule entre les deux et comme elle s'annule en ça veut dire que

[mathilde98]

Mais on est obligé de faire comme ca une disjonction des cas?
Et je ne comprends pas pourquoi Un est compris entre 0 et 1...

[mathilde98]

En fait je ne comprends pas vraiment la disjonction de cas que vous avez fait...
Car si je comprends vous avez divisé par x car x est de toutes façons supérieur à 0
Mais après pourquoi quand x est inférieur à 1 alors ca marche?
Et après je ne vois pas pourquoi Montrer tout ça nous permet d affirmer que la fonction est négative en 0 et positive Un

[Ben314]

La "disjonction de cas", elle est juste là pour rendre la preuve plus rapide.
A la place, on pourrait parfaitement étudier la fonction pour montrer qu'elle est positive sur [0,+oo[. Et il y a surement d'autre faons de procéder pour montrer ce résultat.
Là, c'est une disjonction de cas qui 'est venu à l'esprit vu que ça permettait de conclure en deux lignes, c'est tout...
Aprés, je vois pas ce que tu comprend pas dans le cas où x0, on a donc et d'un autre coté, comme .

Concernant le fait que est entre 0 et 1, c'est la même chose que pour la question 1), mais en étant un peu plus précis : à la question 1) tu as montré que donc est entre 0 et 1.
En fait on peut même faire mieux : donc est entre 0 et 1/n ce qui peret immédiatement d'en déduire que tend vers 0 (théorème des gendarmes)

[mathilde98]

Mais justement je ne comprends pas pourquoi montré que fn(1)=n qui est supérieur à 0 montre que Un est compris entre 0 et 1
De même quand vous dites que Un est compris entre 0 et 1/n....

et pour la monotonie je ne comprends pas pourquoi votre démonstration permet de dire que la suite est négative pour x=0 et positive pour x supérieur à 0...

[Ben314]

Tu as jamais fait d'étude de fonctions ?
La fonction fn, on sait qu'elle est continue et strictement croissante et tu en déduit que, si tu as deux réels a et b tels que fn(a)0 alors il existe un unique x entre a et b tel que fn(x)=0.
C'est le théorème des valeurs intermédiaires qui te prouve qu'il y a au moins un tel x et c'est la croissance stricte qui te prouve qu'il est unique. Au Lycée, on évoque des fois le "théorème de la bijection", mais c'est exactement la même chose.

Sinon, ce n'est pas du tout la suite qui est négative, c'est la fonction fn qui est négative en x=0 (elle vaut -1) et qui est positive en x=1 (elle vaut n) donc elle s'annule pour un certain x entre 0 et 1.
Sauf que le x où elle s'annule, par définition, c'est Un donc Un est entre 0 et 1.

[mathilde98]

ah oui d'accord je comprends! :) mercii!!
Mais alors comment vous avez fait pour trouver après qu'elle était même comprise entre 0 et 1/n ?
ce qui me permet ensuite de dire que sa limite est 0

et sinon je suis désolée mais pour les variations je ne comprends vraiment pas trop comment vous montrez les variations de la suite Un

[Ben314]

TOUT repose sur le truc du message précédent : comme fn est strictement croissante et continue, si on a fn(a)0 alors fn s'annule entre a et b, ce qui veut dire que Un est entre a et b.
- Si a=0 et b=1 on a bien fn(0)=-10 donc Un est entre 0 et 1
- Si a=0 et b=1/n alors fn(a)=-10 donc Un est entre 0 et 1/n.
- Si et b=1 alors fn(a)0 donc Un est entre et 1

[mathilde98]

TOUT repose sur le truc du message précédent : comme fn est strictement croissante et continue, si on a fn(a)0 alors fn s'annule entre a et b, ce qui veut dire que Un est entre a et b.
- Si a=0 et b=1 on a bien fn(0)=-10 donc Un est entre 0 et 1
- Si a=0 et b=1/n alors fn(a)=-10 donc Un est entre 0 et 1/n.
- Si et b=1 alors fn(a)0 donc Un est entre et 1

D accord ca je comprends ce que vous écrivez mais je suis vraiment Desolee car je n arrive pas a comprendre les variations de Un..;)

Car après le reste est facile si Un est compris entre 0 et 1/n alors Un converge car est bornée et monotone et elle converge vers 0 c est bien ca?

Mais vraiment la monotonie je vous assure que j essaye de comprendre mais la j y arrive pas...