Dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Padawan
- Messages: 2
- Enregistré le: 10 Déc 2015, 22:01
-
par Padawan » 10 Déc 2015, 22:23
Salut !
J'ai besoin d'aide pour une bête dérivée ! Je galère vraiment. Voilà le truc :
Je dois dériver chacune des deux expressions par x* et y* sachant que x*=x/D et y*=y/D.
Pour simplifier les calculs, j'ai d(L/D)/dx*=1 et d(T/D)/dy*=1.
En fait, je sais pas quand et comment utiliser ces deux égalités pour simplifier mes dérivées.
Si vous pouviez me mettre sur la voie pour la première dérivée, ça serait cool !
Merci d'avance
-
mathelot
par mathelot » 10 Déc 2015, 23:14
tu peux préciser les notations ? pourquoi du "x" à gauche et pas de "x" à droite ?
-
Padawan
- Messages: 2
- Enregistré le: 10 Déc 2015, 22:01
-
par Padawan » 10 Déc 2015, 23:30
mathelot a écrit:tu peux préciser les notations ? pourquoi du "x" à gauche et pas de "x" à droite ?
Le x intervient dans l'expression de L
L = Lo + x
donc j'ai bien du x à droite, il est juste "caché"
(de la même façon, y intervient dans l'expression de T = To + y)
Mais je ne pense pas qu'il faille remplacer L et T par leur expression, sinon on ne peut pas se servir des simplifications
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
par aymanemaysae » 11 Déc 2015, 11:25
Posons:
=\sqrt{\frac{D}{L})
,
=\frac{T^2}{DL})
,
=
, et
=
,
donc on a : u(x)=
=
=
})
=
,
et v(x,y)=
=
^2}{D(L_0+x)})
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
par aymanemaysae » 11 Déc 2015, 12:05
Posons:
,
,
=
, et
=
,
donc on a : u(x)=
=
=
=
,
et v(x,y)=
=
=
^2}{D(L_0^*+x^*)})
,
donc
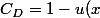 exp(-4v(x,y)) \leftrightarrow 1-C_D=u(x) exp(-4v(x,y)))
=Ln(u(x))+Ln(exp(-4v(x,y)))= -4 v(x,y) + Ln(u(x)))
.
On aussi:
=-\frac{1}{2}\frac{1}{(L_0^*+x^*)^{\frac{3}{2}}})
et
=-(\frac{T0^*+y^*}{L_0^*+x^*})^2)
,
donc
}{1-C_D} = \frac{\frac{\partial{u}}{\partial{x*}}(x)}{u(x)} -4 \frac{\frac{\partial{v}}{\partial{x*}}(x,y)}{v(x,y)} \leftrightarrow \frac{\partial{C_D}}{\partial{x*}} = (1-C_D)(4 \frac{\frac{\partial{v}}{\partial{x*}}(x,y)}{v(x,y)}-\frac{\frac{\partial{u}}{\partial{x*}}(x)}{u(x)}))
,
donc avec
}{u(x)}=-\frac{1}{2(L_0^*+x^*)} et \frac{\frac{\partial{v}}{\partial{x*}}(x,y)}{v(x,y)}=-\frac{1}{L_0^*+x^*})
,
on a
=(1-C_D)(-\frac{4}{L_0^*+x^*}+\frac{1}{2(L_0^*+x^*)})=-\frac{7}{2(L_0^*+x^*)}(1-C_D)<br />= -\frac{7}{2(L_0^*+x^*)^{\frac{3}{2}}} exp(-4\frac{(T0^*+y^*)^2}{D(L_0^*+x^*)}))
Maintenant, si cette démarche est juste, vous pouvez l'utiliser pour calculer la dérivée par rapport à y*.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
