Injectivité, surjectivité

par **Sarah_** » 31 Oct 2015, 15:56

Bonjour, j'ai un devoir à rendre cependant j'ai quelques difficultés (de base).

Voilà ma fonction

f: R/{1}

R
x

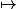
(x+1) /( x-1)

Je dois dans un premier temps montrer qu'elle est injective, simplement je bloque au moment de la simplification.
Voilà ce que j'ai fait :

On veut montrer que

x,y

R/{1}, ( f(x) = f(y)

x=y )

x,y

R/{1}, f(x) = f(y)

(x+1)/(x-1) = (y+1)/(y-1)

Cependant je n'arrive pas à avancer et déduire que x=y

Si quelquun aurait la gentillesse de m'aider..

par **MouLou** » 31 Oct 2015, 16:02

Salut. Tu as essayé de voir a quoi elle ressemblait? Tu verrais qu elle est strictement monotone sur chacune des deux demi droites

par **biss** » 31 Oct 2015, 16:06

je continue
xy+y-x-1=xy-y+x-1
y-x-1=-y+x-1
-2x=-2y
x=y
de rien

par **Sarah_** » 31 Oct 2015, 16:11

Non je n'avais pas essayé, mais je viens de le faire. En effet, elle est bien monotone mais qu'est ce que je dois en déduire ?

Biss, merci beaucoup mais peut tu juste m'expliquer comment as-tu obtenu la première ligne ?

par **biss** » 31 Oct 2015, 16:15

j'ai devellopper a partir de la où tu t'es arreter

par **MouLou** » 31 Oct 2015, 16:17

Ouais ça marhxe bien ça aussi. Il a juste multiplié l égalité par x+1)(y+1).

Bah un fonction strictement monotone est injective c est très simple a monteer. Mais la fait faire attention car elle est strictement monotone sur ]1,+oo[ et sur ]-oo,1[. Donc elle sera injective sur chacun de ces deux intervalles mais pas forcément sur l ensemble tout entier. Bref la méthode proposée par Biss est bien mieux

par **Sarah_** » 31 Oct 2015, 16:24

Ah oui d'accord j'avais pas fait le lien. Merci !

Juste, je dois ensuite fixer y

R et déterminer les éventuels antécedents de y sauf que je ne sais pas comment procéder. Pouvez-vous me donner la méthode de départ svp ?

par **MouLou** » 31 Oct 2015, 16:30

Alors tu peux commencer par essayer de résoudre f(x)=y. Pour y donnè

par **biss** » 31 Oct 2015, 16:37

je continue celui de moulu
((x+1)/(x-1))=y
x+1=(x-1)y
x+1=xy-y
x-xy=-y-1
x(1-y)=-y-1
x=(-y-1)/(1-y)
de rien

par **Sarah_** » 31 Oct 2015, 16:46

Parfait, j'ai trouvé le même résultat merci
Et donc juste pour info, sachant que f est injective et que y à au moins un antécédent, elle est donc surjective, cela suffit-il pour dire que f est bijective ?

par **MouLou** » 31 Oct 2015, 16:51

1 a l infini pour antécédent, attention

par **biss** » 31 Oct 2015, 16:53

Moulou a raison f n'est pas surjective donc pas bijective

par **Sarah_** » 01 Nov 2015, 09:41

Oui autant pour moi merci.

Pendant que j'y suis, j'ai le meme problème avec une autre fonction définie par :

h: R

R
x

x²+x+1

Je n'arrive pas à étudier ni son injectivité, ni sa surjectivité
J'ai essayé quelque chose mais je n'arrive pas à finir

Soit x,y

R tels que h(x)=h(y)
donc x²+x+1 = y²+y+1
x² + x = y²+y
x(1+x) = y(1+y)
x= y(1+y)/(1+x)

par **paquito** » 01 Nov 2015, 10:12

h est représenté par une parabole; elle est donc ni injective, ni surjective!!
:mur:

par **Sarah_** » 01 Nov 2015, 10:15

Va vraiment falloir que je me remettes aux maths sérieusement...

D'accord, merci pour ta réponse rapide mais du coup comment je justifie ça sur ma copie ?

par **paquito** » 01 Nov 2015, 11:04

Dessine une parabole! :briques:

par **zygomatique** » 01 Nov 2015, 19:31

salut

on peut remarquer que f(x) = (x + 1)/(x - 1) = 1 + 2/(x - 1) (forme canonique)

l'injectivité par résolution de f(x) = f(y) est triviale tout comme la stricte monotonie de f sur chacun des intervalles où elle est définie ....

:zen:

Injectivité, surjectivité

Injectivité, surjectivité

Qui est en ligne