Moi je pensait déjà que si A est symétrique alors :
Donc le grdient est :
Calcul d'un gradient
2 messages
- Page 1 sur 1
calcul d'un gradient
par stroke599 » 03 Oct 2015, 09:09
Que vaut le gradient de f: R^n->R telle que =x^{T}*Ax)
ou À est une matrice carrée de taille n*n non symétrique ? Et si A est symétrique que vaut le gradient ?
Moi je pensait déjà que si A est symétrique alors :
)
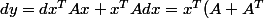dx)
Donc le grdient est :
Moi je pensait déjà que si A est symétrique alors :
Donc le grdient est :
par stroke599 » 03 Oct 2015, 09:34
Sinon je pensait plutôt à calculer f(x+h), d'où:
=(x+h)^{T} A(x+h)=2x^{T}Ah+h^{T}Ah donc f(x+h)-f(x)=2x^{T}Ah+ h^{T}Ah , par consequent notre derivee ici est donc 2x^{T}A)
est notre dérivée si A est symétrique, qu'en pensez vous ?
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :