Calcul de gradient
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 22 Mar 2014, 17:20
par trablazar » 22 Mar 2014, 17:20
Bonjour à tous,
Je viens d'aborder les gradient, le rotationnel et la divergence et j'ai donc quelques exercices dessus.
Dans le premier, je dois calculer les composantes de
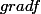
dans plusieurs cas:
Le premier est
=r^n)
avec n entier, supérieur ou égal à 1.
Je pense donc que le r correspond aux coordonnées polaires de la fonction, dois je donc dériver f par rapport à r pour obtenir les composantes de f ? Je dois avouer que je m'attendais à une fonction avec des x et des y que je pourrais tranquillement dériver :ptdr:
Merci d'avoir lu !
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 22 Mar 2014, 19:03
par adrien69 » 22 Mar 2014, 19:03
Tu connais l'expression de r en fonction de x et de y ? C'est quelque chose comme
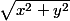
si je ne me trompe pas

-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 22 Mar 2014, 20:05
par trablazar » 22 Mar 2014, 20:05
adrien69 a écrit:Tu connais l'expression de r en fonction de x et de y ? C'est quelque chose comme
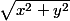
si je ne me trompe pas

Ah oui en effet ! C'était dans le cours mais pas dans l'exo ! Merci beaucoup :we:
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 23 Mar 2014, 14:13
par trablazar » 23 Mar 2014, 14:13
Bonjour,
cette fois-ci on considère

 = \begin{pmatrix} \frac{x}{1+r^2} \\ \frac{y}{1+r^2}+\beta *y^2*z \\ \frac{\alpha *z}{1+r^2}+\beta *\frac{y^3}{3} \end{matrix})
avec
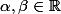
et
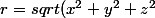)
La premiere question est: Montrer que
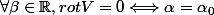
, où
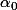
est une constante à déterminer
Du coup j'ai vu que
http://puu.sh/7GgUn.png . Dois-je donc chercher les

et

pour lesquels on a
 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{matrix})
?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Mar 2014, 14:31
par Ben314 » 23 Mar 2014, 14:31
trablazar a écrit:Dois-je donc chercher les

et

pour lesquels on a
 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{matrix})
?
ben... non...
Si on te damande quand est-ce que le
rotationel est nul, ben il faut regarder si... le rotationnel est nul (et pas la fonction de départ)... :mur:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 23 Mar 2014, 14:58
par trablazar » 23 Mar 2014, 14:58
Ben314 a écrit:ben... non...
Si on te damande quand est-ce que le rotationel est nul, ben il faut regarder si... le rotationnel est nul (et pas la fonction de départ)... :mur:
Ah oui j'ai fait une erreur d'ecriture je voulais bien entendu marquer
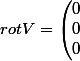
autant pour moi j'ai écris trop vite :soupir2: mais ca doit pas être ca, j'ai commencé les dérivées partielles et certaines ne dépendent pas d'alpha, ce qui m'empêcherais de dire que
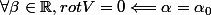
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
