Idéal premier de Z[i]

[Pikachue]

Bonjour,

J'aimerais savoir si (1+i)Z[i] est un idéal premier de Z[i], et si oui, pourquoi.

Merci d'avance.

[Ben314]

Salut,
P'têt ben qu'en regardant qui il y a dans Z[i]/(1+i)Z[i], ça te donnerais la réponse (y'a pas grand monde là dedans...)

[Pikachue]

Le problème c'est que je ne vois pas comment déterminer les éléments de ce quotient... :(

Un élément serait de la forme a + (1+i)Z[i], avec a dans Z[i], mais l'écrire de cette façon ne m'aide pas vraiment.
Alors j'ai essayé de voir ce qu'était (1+i)Z[i] plus précisément.
Z[i]=Z+ iZ, donc si b est dans (1+i)Z[i], il est de la forme
b=(1+i)(c+id) où c et d sont dans Z,
donc b = c + id +ic - d.
Cool, mais ça ne m'aide pas vraiment non plus...

La seule chose que je sais c'est que (1+i)Z[i]=(1-i)Z[i].

Je suppose que le but de regarder ce quotient est de voir si c'est un corps (ou non), ce qui nous dira si c'est, oui ou non, un idéal premier?

Merci beaucoup pour votre réponse!

[Ben314]

Ce n'est pas forcément la façon la plus simple de rédiger, mais sinon, bien sûr que si que ça t'aide.
Lorsque tu écrit que a+ib est dans (1+i)Z[i] ssi il existe c et d dans Z tels que a+ib=c+id+ic-d
le "il existe c et d tels que" te dit que ce qu'il faut faire, c'est résoudre le truc en regardant a et b comme des paramètres et c et d comme des inconnues pour voir quand est-ce qu'il y a des solutions (en fonction de a et b).
Essaye de le faire.

Sinon, vu qu'on peut plonger Z[i] dans Q[i] (voire C si tu préfère) qui est un corps, il était plus simple de dire que a+ib est dans (1+i)Z[i] ssi (a+ib)/(1+i) est dans Z[i] et c'est pas bien compliqué de voir à quoi ça correspond comme condition sur a et b.

Ensuite, tu as le choix, soit tu regarde qui est le quotient Z[i]/(1+i)Z[i] (en fait il n'y a que deux éléments dedans donc c'est pas trop compliqué...), soit tu prend uniquement la définition de "idéal premier" et tu regarde s'il est vrai que, si un produit de deux éléments est dans (1+i)Z[i] alors forcément un des deux termes du produit est dedans : ce n'est pas bien compliqué non plus et si tu as du temps, je t'inciterais bien à le faire aussi...

Ensuite, si tu as tout bien compris, tu peut essayer de regarder si tu arrive à généraliser, c'est à dire à trouver une C.N.S. pour que (a+ib)Z[i] soit un idéal premier (c'est peut-être plus simple avec la deuxième méthode)

[Pikachue]

a+ib est dans (1+i)Z[i] ssi il existe c et d dans Z tq a+ib = c-d +i(d+c)
ssi il existe c et d dans Z tq c-d=a et d+c=b
ssi il existe c et d dans Z tq c=(a+b)/2 et d=(b-a)/2
ssi a et b sont dans Z, de même parité.
Bon, voilà ce que j'ai...

J'ai absolument aucune idée de la façon dont on est censé déterminer Z[i]/(1+i)Z[i], alors on va partir sur la définition.

Je prends a=m+in et b=r+is tq ab est dans (1+i)Z[i].
Après un savant calcul, on trouve ab=mr-ns + i(ms+nr).
On sait que mr-ns et ms+nr sont dans Z, et de même parité.
Il faut montrer que, soit m et n sont dans Z de même parité, soit r et s sont dans Z de même parité.
(Ou je sais pas si c'est plus simple, que la somme sur 2 et la différence sur 2 sont dans Z)
On a que mr-ns+ms+nr = m(r+s)+n(r-s) = 2k avec k dans Z.

Si vous dites que c'est pas compliqué, c'est que je dois pas être bien maline, parce que je ne vois pas trop quoi faire de ça...

[Ben314]

Tu t'y prend pas forcément de la meilleure façon, mais en continuant dans cette logique, tu peut tout à fait t'en sortir :
Déjà, un truc pas con de "logique pure", c'est que pour montre qu'on a P ou Q (deux propositions), c'est souvent pratique de supposer par exemple que est P faux : comme ça, au moins on sait ce qu'on doit montrer...

Donc là, supposons par exemple que m et n n'ont pas la même parité (i.e que m+in n'est pas dans (1+i)Z[i])
- Si m est pair et n impair alors m(r+s)+n(r-s) a la même parité que r-s donc on doit avoir r-s pair c'est à dire r et s de même parité.
- Si m est impair et n pair alors m(r+s)+n(r-s) a la même parité que r+s donc on doit avoir r+s pair c'est à dire r et s de même parité.

Sinon, c'était un peu plus "joli" en raisonnant dans : dire que "m et n ont même parité", ben ça veut dire que
Donc, pour que soit dans il faut (et il suffit) que sauf que, (i.e. les + et les - c'est la même chose) donc

Et comme est un corps, pour qu'un produit soit nul, il faut qu'un des facteurs soit nul.

[Ben314]

Sinon, concernant le "qui" est , une fois que tu as montré que , ça te dit que (en notant la classe de modulo ) :


Donc, si alors et, si alors .

BILAN :

[Pikachue]

D'accord!
J'ai compris toute la première réponse! Merci beaucoup! :we:

Par contre la deuxième, j'ai encore du mal. C'est pas mon truc les quotients d'ensembles. En fait, l'algèbre en général c'est pas mon truc... J'ai jamais rien compris, je comprendrai jamais rien. Désolée si je bloque sur des choses basiques.
Pourquoi a-t-on
?

[Ben314]

Par ce que, par définition du quotient A/I (où A est un anneau et I un idéal), deux éléments x et y de A sont dans la "même classe modulo I" lorsque x-y est dans I.
Donc ici, dire que a+ib et c+id sont dans la même "classe modulo (1+i)Z[i]", ben ça veut précisément dire que (a-c)+i(b-d) est dans (1+i)Z[i].

Je sais pas comment on te l'a présenté, peut être en écrivant qu'une "classe modulo I", c'est un ensemble de la forme x+I avec x dans A, mais ça revient totalement au même vu que dire que y est dans x+I, ben ça veut précisément dire que y-x est dans I.

[Pikachue]

Ah d'accord! Je n'ai pas vu les choses sous cet angle, et c'est vrai que ça en revient au même...

Une dernière question si possible :

Le but de tout ça était de montrer que
où .
Pour ça, mon prof m'a fait remarqué que, si est premier (d'où ma question à la base, parce que j'ai montré que si est premier, alors l'intersection l'est), alors on a l'égalité parce que .

Mais en y réfléchissant, ce n'est pas l'inverse, justement?
C'est-à-dire que, , donc divise 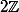qui lui est un idéal premier de Z, ce qui donnerait l'égalité?

Du coup il n'y aurait pas eu besoin de montrer que était premier. (Même si je préfère quand même l'avoir fait, je n'ai pas perdu mon temps, loin de là)

[Ben314]

Avant de regarder le coté un peu "théorique" proposé (qui est surement intéressant), je me permet quand même de dire que de faire "de la théorie", c'est un peu "utiliser un marteau pour écraser une mouche" :

En utilisant que et exclusivement que la définition de (1+i)Z[i] (donc sans même savoir que c'est un idéal, ni que Z[i] est un anneau, ni... rien...), le problème posé se ramène à savoir quels sont les entiers n qu'on peut écrire sous la forme
n=(1+i)(a+ib) avec a et b dans Z
c'est à dire n=a-b (partie réelle) et a+b=0 (partie imaginaire) en bref, b=-a et n=2a : et... c'est fini...

Bon, après, concernant la "théorie" que tu écrit, ça me semble pas clair, mais je sais pas ce que tu as vu concernant les idéaux...
Par exemple, partant du constat que , pour en déduire immédiatement quelque chose, ce qui me vient à l'esprit, c'est d'utiliser le fait que est un idéal maximal de Z plutôt que le fait que c'est un idéal premier de Z.
Bon, après, vu que dans Z c'est la même chose, ça change pas bien grand chose, sauf que pour moi, c'est vraiment la maximalité qui te permet en claquant des doigts d'en déduire que que c'est soit 2Z, soit Z tout entier.

Par contre, ce que je confirme, c'est que de savoir que est un idéal premier (et donc maximal) de Z et qu'il contient un autre idéal I, je pense pas qu'on en déduise grand chose (par exemple 5Z est maximal et contient 20Z donc... pas grand chose...)

[Pikachue]

J'ai simplement essayé de suivre les indications qu'on m'avait donné... Mais c'est vrai que montrer l'égalité n'était pas difficile du tout, quand on y réfléchit... J'aurais dû y penser.

Je comprends pourquoi vous pensez plutôt à la maximalité. Je pensais que ça pouvait aussi se faire avec le fait que c'est un idéal premier, mais j'ai peut-être mal compris ce que mon professeur m'a expliqué.

Il me semble bien cependant que maximal implique premier, mais pas l'inverse.

[Ben314]

J'ai simplement essayé de suivre les indications qu'on m'avait donné... Mais c'est vrai que montrer l'égalité n'était pas difficile du tout, quand on y réfléchit... J'aurais dû y penser.
Je comprends pourquoi vous pensez plutôt à la maximalité. Je pensais que ça pouvait aussi se faire avec le fait que c'est un idéal premier, mais j'ai peut-être mal compris ce que mon professeur m'a expliqué.
Il me semble bien cependant que maximal implique premier, mais pas l'inverse.

De toute façon, comme des tas d'autres exercices, il y a des tas de façons de le résoudre utilisant plus ou moins de théorie et, quand on a le temps, c'est super pas con d'essayer de "faire le tour" de toute les méthodes, de la plus "artisanale" à la plus "théorique" pour constater que, ou bien c'est à peu prés la même chose rédigé différemment ou alors... pas du tout la même chose.

Mais, a mon avis, c'est forcément très "formateur" vu que ça fait bien comprendre qu'il y a toujours plusieurs façon de voir un même problème et que la résolution "artisanales" du problème permet souvent d'un peu "démystifier" un nouveau concept.

Sinon, je confirme qu'effectivement, on a en général uniquement l'implication "maximal => premier", sauf que, dans le cas général des anneaux principaux (donc dans le cas cas particulier des anneaux euclidiens donc dans les cas très particuliers de Z et de Z[i] qui sont euclidiens), il y a... équivalence entre les deux notions.