Intégrale double de e^(-y/x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par chocolatbleu » 01 Avr 2015, 13:59
par chocolatbleu » 01 Avr 2015, 13:59
Bonjour,
Je n'arrive pas à calculer l'intégrale double de e^(-y/x) avec comme bornes pour x : 2y à 2 et pour y : 0 à 1. J'ai changé les bornes des intégrales, ce qui me donne pour x : 0 à 2 et pour y : 0 à x/2 , mais ça ne m'aide pas spécialement. J'ai essayé plusieurs méthodes avec une amie et j'arrive toujours à [1-e^(-1/2)]/2 alors que la réponse devrait être 1 car quand on cherche l'aire à calculer en faisant un graphique, l'ensemble est égal à la moitié d'un rectangle de 1 unité de côté sur 2.
Savez-vous m'aider ?

-
Godfrey
- Membre Naturel
- Messages: 51
- Enregistré le: 04 Mar 2015, 10:24
-
 par Godfrey » 01 Avr 2015, 14:53
par Godfrey » 01 Avr 2015, 14:53
Salut,
Sous quelles conditions peux-tu permuter les intégrales ?
Quand on a une intégrale où l'un des paramètres dépend de l'autre, c'est toujours mieux d'utiliser des indicatrices pour se ramener à un domaine fixe.
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Avr 2015, 15:02
par siger » 01 Avr 2015, 15:02
bonjour
oui on peut peut-etre t'aider ....
d'ou vient cette "interpretation geometrique" ?
Inegrale (de a à b) (f(x) dx) est effectivement egale a l'aire comprise entre l'axe des abscisses, a , b et ......la COURBE f(x)
mais par la courbe representant ici la fonction obtenue par l'integration sur y
dans ton interpretation ou est cette courbe ? ce n'est certainement pas la droite que tu as tracée.......
 par chocolatbleu » 01 Avr 2015, 15:05
par chocolatbleu » 01 Avr 2015, 15:05
Godfrey a écrit:Salut,
Sous quelles conditions peux-tu permuter les intégrales ?
Quand on a une intégrale où l'un des paramètres dépend de l'autre, c'est toujours mieux d'utiliser des indicatrices pour se ramener à un domaine fixe.
J'ai peur de ne pas vraiment comprendre votre question donc dites-le moi si je réponds à côté :lol3:
En traçant le graphique des intégrales de base, je trouve l'aire à calculer et je peux trouver d'autres bornes que celles de base en fonction du graphique. J'examine le graphique et je réécris les bornes différemment en fonction de l'aire à calculer.
 par chocolatbleu » 01 Avr 2015, 15:22
par chocolatbleu » 01 Avr 2015, 15:22
siger a écrit:bonjour
oui on peut peut-etre t'aider ....
d'ou vient cette "interpretation geometrique" ?
Inegrale (de a à b) (f(x) dx) est effectivement egale a l'aire comprise entre l'axe des abscisses, a , b et ......la COURBE f(x)
mais par la courbe representant ici la fonction obtenue par l'integration sur y
dans ton interpretation ou est cette courbe ? ce n'est certainement pas la droite que tu as tracée.......
Cette "interprétation géométrique" vient de ma méthode à appliquer ... C'est ce qu'on nous a appris à faire lorsqu'une intégrale n'est pas intégrable dans ses bornes. Ici, e^(-y/x) est intégrable dans les bornes de départ mais je ne voyais pas du tout comment faire donc j'ai changé les bornes.
Voilà le calcul que j'ai fait en premier.

Après j'ai essayé en posant -y/x = f et donc -dy/x = df mais j'obtiens la même réponse qu'avec mon premier calcul.
Mon problème c'est que je ne sais pas comment m'occuper de e^(-y/x) dans les intégrales. J'ai fait un changement de bornes mais je ne suis pas sure non plus qu'il fallait le faire.
Comme énoncé j'ai : Justifier l'existence des intégrales suivantes et calculer leur valeur:

-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Avr 2015, 15:27
par siger » 01 Avr 2015, 15:27
RE
le probleme n'est pas le changement de bornes.....
" la réponse devrait être 1 car quand on cherche l'aire à calculer en faisant un graphique, l'ensemble est égal à la moitié d'un rectangle de 1 unité de côté sur 2 ".?????
 par chocolatbleu » 01 Avr 2015, 15:35
par chocolatbleu » 01 Avr 2015, 15:35
siger a écrit:RE
le probleme n'est pas le changement de bornes.....
" la réponse devrait être 1 car quand on cherche l'aire à calculer en faisant un graphique, l'ensemble est égal à la moitié d'un rectangle de 1 unité de côté sur 2 ".?????
En traçant mes bornes, j'obtiens un graphique qui me délimite une aire. Cette aire je dois la calculer et ici, si on regarde le graphique, l'aire à calculer (en gris), c'est la moitié de l'aire du rectangle rose qui fait 2 unités de long sur 1 unité de large. donc 2.1=2 et 2/2=1. Donc mon aire grise fait 1 unité² .

-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Avr 2015, 16:11
par siger » 01 Avr 2015, 16:11
Re
plutot que de te focaliser sur les bornes, revois la definition des integrales et des aires
l'aire "en gris" qui figure sur ton graphique est egale a l'integrale de 0 a 2 (x*dx) et n' a rien a voir avec une quelconque exponentielle .........
ou alors toutes les integrales doubles de 0 a 1 et de 2y a 2, ont toutes la même valeur (=1) quelque soit la fonction f(x,y) a integrer.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 01 Avr 2015, 16:18
par Pythales » 01 Avr 2015, 16:18
chocolatbleu a écrit:Bonjour,
Je n'arrive pas à calculer l'intégrale double de e^(-y/x) avec comme bornes pour x : 2y à 2 et pour y : 0 à 1. J'ai changé les bornes des intégrales, ce qui me donne pour x : 0 à 2 et pour y : 0 à x/2 , mais ça ne m'aide pas spécialement. J'ai essayé plusieurs méthodes avec une amie et j'arrive toujours à [1-e^(-1/2)]/2 alors que la réponse devrait être 1 car quand on cherche l'aire à calculer en faisant un graphique, l'ensemble est égal à la moitié d'un rectangle de 1 unité de côté sur 2.
Savez-vous m'aider ?

Ce qui est égal à 1, c'est



-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Avr 2015, 16:31
par Ben314 » 01 Avr 2015, 16:31
Salut,
Le problème, c'est que tu utilise le fait que le calcul d'une intégrale correspond à un calcul d'aire dans un contexte où c'est (assez clairement) faux.
Une intégrale
simple du style
dt)
correspond effectivement à un calcul d'aire (dans le cas où la fonction f est positive) c'est l'aire de la surface
\text{ t.q. }a<x<b\text{ et }0<y<f(x)\})
contenue dans R^2.
Par contre, le calcul d'une intégrale double du style
dxdy)
(où D est une partie de R^2) correspond à un calcul de
volume (dans le cas où la fonction f est positive) c'est le volume de la partie
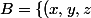\text{ t.q. }(x,y)\in D\text{ et }0<z<f(x,y)\})
contenue dans R^3.
Visiblement, tu raisonne comme si
dxdy)
donnait la surface de la partie D ce qui est assez absurde vu que ça voudrait dire que la valeur de I ne dépend que de D et pas de la fonction f...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Avr 2015, 16:55
par siger » 01 Avr 2015, 16:55
re
merci "Ben314" d'avoir exposé clairement ce qu'un "non-matheux" comme moi n'arrivait pas a expliquer clairement
 par chocolatbleu » 01 Avr 2015, 19:50
par chocolatbleu » 01 Avr 2015, 19:50
Oui c'est vrai, je me suis trompée là-dedans, désolée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités




