Fonction ln et exp
31 messages
- Page 1 sur 2 - 1, 2
Fonction ln et exp
Bonjour, j'ai un exercice a résoudre pour un devoir maison mais je ne comprend pas l'exercice.
Voici l'exercice:
On considère la fonction f définie sur ]0, +infini[ par: f(t)= (ln t)²
On appelle C la courbe représentative de f dans un repère orthonormal du plan.
1) Quelle est la limite de f(t) lorsque t tend vers 0 ?
Que peut-on en déduire pour la courbe C ?
2) Donner la limite de f(t) en +infini.
3) Montrer que la dérivée de f est définie, pour tout x de ]0, +infini[, par: f'(t)= 2 x ln t/t
En déduire le sens de variation de f.
4) Dresser le tableau de variation de f.
5) Tracer la courbe C.
Merci de m'aider.
Voici l'exercice:
On considère la fonction f définie sur ]0, +infini[ par: f(t)= (ln t)²
On appelle C la courbe représentative de f dans un repère orthonormal du plan.
1) Quelle est la limite de f(t) lorsque t tend vers 0 ?
Que peut-on en déduire pour la courbe C ?
2) Donner la limite de f(t) en +infini.
3) Montrer que la dérivée de f est définie, pour tout x de ]0, +infini[, par: f'(t)= 2 x ln t/t
En déduire le sens de variation de f.
4) Dresser le tableau de variation de f.
5) Tracer la courbe C.
Merci de m'aider.
Salut !
Avant tout, tu peux remarquer que f est la composée de la fonction "logarithme népérien" par la fonction "carré" (ca peut t'aider pour des calculs de limites, variations etc).
Où bloques-tu ?
Avant tout, tu peux remarquer que f est la composée de la fonction "logarithme népérien" par la fonction "carré" (ca peut t'aider pour des calculs de limites, variations etc).
Où bloques-tu ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
jujutt42 a écrit:Bonjour, j'ai un exercice a résoudre pour un devoir maison mais je ne comprend pas l'exercice.
Voici l'exercice:
On considère la fonction f définie sur ]0, +infini[ par: f(t)= (ln t)²
On appelle C la courbe représentative de f dans un repère orthonormal du plan.
1) Quelle est la limite de f(t) lorsque t tend vers 0 ?
Que peut-on en déduire pour la courbe C ?
2) Donner la limite de f(t) en +infini.
3) Montrer que la dérivée de f est définie, pour tout x de ]0, +infini[, par: f'(t)= 2 x ln t/t
En déduire le sens de variation de f.
4) Dresser le tableau de variation de f.
5) Tracer la courbe C.
Merci de m'aider.
Vas-y étapes par étapes :
Or
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
On a fait un "changement de variable" pour calculer la limite.
On utilise le fait suivant : si on note la fonction carré ,
,  .
.
Ainsi = \lim_{t\to 0^+ } (C\circ \ln )(t) = \lim_{t\to 0^+ } C( \ln(t) ) = \lim_{ x\to - \infty } C(x )) en posant
en posant ) .
.
On utilise le fait suivant : si on note la fonction carré
Ainsi
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Tu peux commencer par ce que j'ai dit :
Ne me demande pas ce qu'il faut que tu notes : ce que tu écrit traduit la compréhension que tu as de la question.
Tu as juste à comprendre le principe après, tu pourras rédiger ça tout seul à ta façon :
Tu sais que = -\infty) . Posons
. Posons ) . Alors
. Alors
[CENTER])^2=\lim_{x\to -\infty} x^2) [/CENTER]
[/CENTER]
:+++:
capitaine nuggets a écrit:Vas-y étapes par étapes :.
Ordonc
.
Ne me demande pas ce qu'il faut que tu notes : ce que tu écrit traduit la compréhension que tu as de la question.
Tu as juste à comprendre le principe après, tu pourras rédiger ça tout seul à ta façon :
Tu sais que
[CENTER]
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Oui, biensûr :we:
2) Pour la limite en , c'est le même raisonnement.
, c'est le même raisonnement.
Que vaut) ? Que vaut
? Que vaut  ?
?
Déduis-en ta limite en .
.
3) Il s'agit de calculer la dérivée d'une composée de fonctions.
Si et
et  désignent deux fonctions définies et dérivables sur
désignent deux fonctions définies et dérivables sur  , quelle est la dérivée de
, quelle est la dérivée de 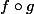 ?
?
2) Pour la limite en
Que vaut
Déduis-en ta limite en
3) Il s'agit de calculer la dérivée d'une composée de fonctions.
Si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:2) Pour la limite en, c'est le même raisonnement.
Que vaut? Que vaut
?
Déduis-en ta limite en.
Voilà une autre formulation si tu veux (mais c'est lourd comme écriture) :
[CENTER]
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
