Nb complexes - exp(exp(x))
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
H4rper
- Messages: 4
- Enregistré le: 24 Sep 2015, 18:39
-
 par H4rper » 24 Sep 2015, 18:50
par H4rper » 24 Sep 2015, 18:50
Bonjour à tous,
On demande de déterminer le module et l'argument du nombre complexe :
exp(exp(i theta))
Avez vous une idée de quel outil utiliser pour résoudre ce problème ? (Euler, moivre, etc..)
Bien cordialement


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Sep 2015, 19:01
par chan79 » 24 Sep 2015, 19:01
salut
tu as
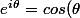+i\,sin(\theta))

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Sep 2015, 19:07
par chan79 » 24 Sep 2015, 19:07
salut
tu as
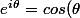+i\,sin(\theta))
-
H4rper
- Messages: 4
- Enregistré le: 24 Sep 2015, 18:39
-
 par H4rper » 24 Sep 2015, 19:11
par H4rper » 24 Sep 2015, 19:11
Oui, mais ma question est : exp(exp(i theta))
On pose x=theta, ça donne :
Exp(cos(x)+isin(x)) et la je bloque..

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Sep 2015, 19:33
par chan79 » 24 Sep 2015, 19:33
H4rper a écrit:Oui, mais ma question est : exp(exp(i theta))
On pose x=theta, ça donne :
Exp(cos(x)+isin(x)) et la je bloque..
Applique:
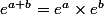
-
H4rper
- Messages: 4
- Enregistré le: 24 Sep 2015, 18:39
-
 par H4rper » 24 Sep 2015, 19:53
par H4rper » 24 Sep 2015, 19:53
chan79 a écrit:Applique:
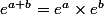
J'en suis arrivé à exp(cosx) x exp(isinx)
Sauf que je bloque ici depuis le début, je sais transformer exp(ix)=cosx+isinx avec x=sinx mais par contre j'ai aucune idée pour développer exp(cosx) vu qu'il n'y a pas d'indice i..
-
mathelot
 par mathelot » 24 Sep 2015, 20:03
par mathelot » 24 Sep 2015, 20:03
-
H4rper
- Messages: 4
- Enregistré le: 24 Sep 2015, 18:39
-
 par H4rper » 24 Sep 2015, 20:26
par H4rper » 24 Sep 2015, 20:26
mathelot a écrit:) e^{i sin(\theta)})
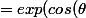) \, \left( cos( sin(\theta))+i sin(sin(\theta)) \right))
Je crois que je me suis trop pris la tête en gros ça veut dire que :
|exp(exp(itheta))| = exp(cos(theta))
Arg(exp(exp(itheta)) = sin (theta)
Pour tout theta appartenant à R
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités