voici le probleme: 8 pour cent des clients d'une banque gardent un solde minimun a 500 dollars dans leur compte. Quelle est la probabilité que, dans un échantillon aléatoire de 100 client,
a) exactement 7 client gardent un solde minimum de 500 dollars
b) moins de 10 gardent un solde minimum de 500 dollars
Je ne sais plus quoi faire pour ce numero... comemnt faire si je n'ai pas la moyenne ou l'écart type?
Merci
Probabilités
4 messages
- Page 1 sur 1
par mathelot » 20 Fév 2015, 07:07
bonjour,
Soit X le nombre de clients qui garde un solde minimum de 500 dollars
X suit une loi binomiale de paramètres n=100,p=0.08
On pose
)
=np=100 \times 0.08 = 8)
=npq=100 \times 0.08 \times 0.92=7.36)
=\sqrt{V(X)}=2.7129)
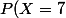=(_7^{100}) p^7 q^{93})
calculé ainsi, le produit est comme une forme indéterminée (F.I)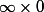
,
difficilement calculable, car le coefficient binomial est monstrueusement grand et les produits de probas excessivement petits.
=\frac{100 \times 99 \times 98 \times 97 \times 96 \times 95 \times 94}{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times7})
on approche cette loi binomiale par une loi de Poisson (valable si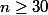
et 
)
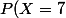\sim \frac{\lambda^k}{k!} \, e^{-\lambda})
avec
et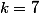 
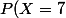 \sim 0.139586)
 \sim e^{- \lambda} \sum_{k=0}^{9} \, \frac{\lambda^k}{k!} \sim 0.4529)
remarque :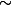
signifie "peu différent de"
pour les mesures (nbrs réels) ou "suivre la loi de proba" pour les variables aléatoires.
sauf erreur ....
Soit X le nombre de clients qui garde un solde minimum de 500 dollars
X suit une loi binomiale de paramètres n=100,p=0.08
On pose
calculé ainsi, le produit est comme une forme indéterminée (F.I)
difficilement calculable, car le coefficient binomial est monstrueusement grand et les produits de probas excessivement petits.
on approche cette loi binomiale par une loi de Poisson (valable si
avec
remarque :
pour les mesures (nbrs réels) ou "suivre la loi de proba" pour les variables aléatoires.
sauf erreur ....
par the_bongker » 20 Fév 2015, 14:21
mathelot a écrit:bonjour,
Soit X le nombre de clients qui garde un solde minimum de 500 dollars
X suit une loi binomiale de paramètres n=100,p=0.08
On pose
calculé ainsi, le produit est comme une forme indéterminée (F.I)
difficilement calculable, car le coefficient binomial est monstrueusement grand et les produits de probas excessivement petits.
on approche cette loi binomiale par une loi de Poisson (valable si
avec
remarque :
pour les mesures (nbrs réels) ou "suivre la loi de proba" pour les variables aléatoires.
sauf erreur ....
Merci bcp. Une dernière question monsieur, pouvez-vous me dire quand appliquer la loi hypergéométrique?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :