Difficulté matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 00:29
par trablazar » 04 Jan 2015, 00:29
Bonjour,
J'ai récemment eu un partiel que j'ai complètement foiré, et j'aimerais comprendre l'un des exercices pour ne pas réitérer la chose :mur: Voici l'exercice:
http://puu.sh/e26sV/d0cc622d95.jpgVoici ce que j'ai fait:
1)

2)a) J'ai dit que c'etait une matrice dont chaque colonne était de type

b) Puisque chaque colonne a un coefficient (le vecteur U) commun, alors toutes les colonnes sont liées donc le rang est égal à 1
3) La ca commencer à chier dans la colle : j'ai dit que dim A = rang A + dim(Im(A)) Donc dim(Im(A))= n-1
Donc dim(Ker(A)) = 1 et 0 est une solution évidente donc il n'y a que 0 puisque dim = 1.
Pour
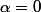
, on a : A = 0 donc on a
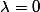
valeur propre de multiplicité n car le polynome carac. est égal à
=s^n)
4) Si

, on a :
A²=-A
A + A² = 0
A (I + A) = 0
I + A = 0
Donc I + A non inversible car 0 valeur propre de I +A
5) Si

, on a :


 = 0)

Et la je sais pas...
Quelqu'un pourrait-il m'aider ?
Merci beaucoup

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 04 Jan 2015, 09:23
par fatal_error » 04 Jan 2015, 09:23
hello,
pour 5,
la question précédente, on dit (I+A) non inversible pour alpha=-1, et celle là t'as alpha!=-1, du coup on a envie de supposer (I+A) inversible (faut le prouver, mais j'ai pas regardé la question d'avant)
du coup on peut multiplier gauche et à droite par (I+A) avec équivalence
I = (I+A)(I+kA) = I + (k+1)A + kA^2 = I + (k+1+alpha)A
et on déduit k
la vie est une fête

-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 10:57
par trablazar » 04 Jan 2015, 10:57
fatal_error a écrit:hello,
pour 5,
la question précédente, on dit (I+A) non inversible pour alpha=-1, et celle là t'as alpha!=-1, du coup on a envie de supposer (I+A) inversible (faut le prouver, mais j'ai pas regardé la question d'avant)
du coup on peut multiplier gauche et à droite par (I+A) avec équivalence
I = (I+A)(I+kA) = I + (k+1)A + kA^2 = I + (k+1+alpha)A
et on déduit k
Salut,
Du coup tu pars de l'égalité
^{-1} = I + kA)
, et, en supposant I + A inversible, tu multiplies des deux coté par I + A ? J'arrive à

Du coup pour la 6) Je fais:
a)


J'additionne par
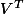
des deux cotés
 = V^T (I + M^{-1} A))
Donc si

donc non inversible car 0 est valeur propre
Après pour montrer que c'est inversible quand b != -1, je ne sais pas par ou commencer: j'ai trouvé que b+1 est valeur propre de

et que V^T est vecteur propre. Or, b+1 != 0 mais cela ne me dit pas qu'il n'y a pas d'autres valeurs propres, dont une est égale à 0...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 04 Jan 2015, 11:06
par Pythales » 04 Jan 2015, 11:06
fatal_error a écrit:hello,
pour 5,
la question précédente, on dit (I+A) non inversible pour alpha=-1, et celle là t'as alpha!=-1, du coup on a envie de supposer (I+A) inversible (faut le prouver, mais j'ai pas regardé la question d'avant)
du coup on peut multiplier gauche et à droite par (I+A) avec équivalence
I = (I+A)(I+kA) = I + (k+1)A + kA^2 = I + (k+1+alpha)A
et on déduit k
Plus exactement

-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 11:15
par trablazar » 04 Jan 2015, 11:15
-
Eogel
- Messages: 4
- Enregistré le: 04 Jan 2015, 11:38
-
 par Eogel » 04 Jan 2015, 11:58
par Eogel » 04 Jan 2015, 11:58
" 4) Si \alpha = -1 , on a :
A²=-A
A + A² = 0
A (I + A) = 0
I + A = 0
Attention. En écrivant ça tu laisses penser, que soit l'anneau des matrices est intègre, et alors comme A est non nulle, I+A l'est (ce qui est moche), soit la matrice A est inversible, ce qui est faux (rang =1).
Quand tu arrives à A(I+A)=0, il faut dire "par l'absurde, si I+A était inversible, alors en multipliant par son inverse, A serait nulle, ce qui est proscrit" et donc t'as le résultat.Donc I + A non inversible car 0 valeur propre de I +A "
D'ailleurs, si I + A = 0, I + A est directement non inversible puisque c'est la matrice nulle" A ( k + 1 + k \alpha ) = 0 D'ailleurs la on a le droit de dégager la A ? Elle inversible ?
k + 1 + k \alpha = 0 "
Non, A n'est pas inversible, car son rang est différent de n. (rg (A) = n dim ker A = 0 ker A = 0 (dimension finie) A inversible) Mais tu as le droit d'écrire ces deux lignes car tu utilises ici un produit entre un scalaire et une matrice, et non entre deux matrices, donc c'est sous la forme aA = 0, et ici tu peux déduire a = 0 (il suffit de regarder les coefficients de la matrice aA, et comme A est non nulle, en identifiant sur un coefficient non nul de A, on en déduit a = 0)
Attention aux notations : on écrit de la même manière le produit AB (produit entre deux éléments de l'algèbre) et le produit aA (loi externe entre le scalaire et l'élément de l'algèbre des matrices) mais ils sont bien différents!J'espère t'avoir aidé

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2015, 12:05
par Carpate » 04 Jan 2015, 12:05
trablazar a écrit:3) j'ai dit que dim A = rang A + dim(Im(A)) Donc dim(Im(A))= n-1
Donc dim(Ker(A)) = 1 et 0 est une solution évidente donc il n'y a que 0 puisque dim = 1.
Pour
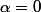
, on a : A = 0 donc on a
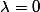
valeur propre de multiplicité n car le polynome carac. est égal à
=s^n)
Petit retour sur la 3)
dim A = rang A + dim(Im(A))dim(A) = n^2 et non n !
D'où sort cette règle ?
Dim(ker(A)) + rang(A) = n
dim(ker(A)) = n-1
dim(Im(f) = rang(A) = 1
v.p. de A :V et

tels que :

on multiplie à gauche par A
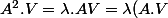=\lambda^2 V)



:
 = 0)
0 et

valeurs propres de A
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 12:05
par trablazar » 04 Jan 2015, 12:05
Eogel a écrit:" 4) Si \alpha = -1 , on a :
A²=-A
A + A² = 0
A (I + A) = 0
I + A = 0
Attention. En écrivant ça tu laisses penser, que soit l'anneau des matrices est intègre, et alors comme A est non nulle, I+A l'est (ce qui est moche), soit la matrice A est inversible, ce qui est faux (rang =1).
Quand tu arrives à A(I+A)=0, il faut dire "par l'absurde, si I+A était inversible, alors en multipliant par son inverse, A serait nulle, ce qui est proscrit" et donc t'as le résultat.Donc I + A non inversible car 0 valeur propre de I +A "
D'ailleurs, si I + A = 0, I + A est directement non inversible puisque c'est la matrice nulle" A ( k + 1 + k \alpha ) = 0 D'ailleurs la on a le droit de dégager la A ? Elle inversible ?
k + 1 + k \alpha = 0 "
Non, A n'est pas inversible, car son rang est différent de n. (rg (A) = n dim ker A = 0 ker A = 0 (dimension finie) A inversible) Mais tu as le droit d'écrire ces deux lignes car tu utilises ici un produit entre un scalaire et une matrice, et non entre deux matrices, donc c'est sous la forme aA = 0, et ici tu peux déduire a = 0 (il suffit de regarder les coefficients de la matrice aA, et comme A est non nulle, en identifiant sur le coefficient non nul de A, on en déduit a = 0)
Attention aux notations : on écrit de la même manière le produit AB (produit entre deux éléments de l'algèbre) et le produit aA (loi externe entre le scalaire et l'élément de l'algèbre des matrices) mais ils sont bien différents!J'espère t'avoir aidé

Salut à toi !
Tout d'abord je t'avouerai qu'avant toi je n'avais jamais entendu parler d'anneau de matrice ! Mais sinon ton raisonnement par l'absurde est en effet indispensable, je n'y avais pas pensé...
Mais tu as le droit d'écrire ces deux lignes car tu utilises ici un produit entre un scalaire et une matrice, et non entre deux matrices, donc c'est sous la forme aA = 0, et ici tu peux déduire a = 0 (il suffit de regarder les coefficients de la matrice aA, et comme A est non nulle, en identifiant sur le coefficient non nul de A, on en déduit a = 0)
Mais oui tout simplement ! C'est vrai que je butais un peu dessus, me demandant pourquoi j'y trouvais à redire :ptdr: En tout cas merci, tu m'as en effet beaucoup aidé :we:
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 12:10
par trablazar » 04 Jan 2015, 12:10
Carpate a écrit:Petit retour sur la 3)
dim A = rang A + dim(Im(A))dim(A) = n^2 et non n !
D'où sort cette règle ?
Dim(ker(A)) + rang(A) = n
dim(ker(A)) = n-1
dim(Im(f) = rang(A) = 1
v.p. de A :V et

tels que :

on multiplie à gauche par A
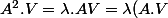=\lambda^2 V)



:
 = 0)
0 et

valeurs propres de A
Ah oui je me rends compte que j'ai tout mélangé pour le coup...
Je ne savais pas par ou commencer, mais c'est vrai que poser

est le plus logique! Merci beaucoup !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2015, 12:22
par Carpate » 04 Jan 2015, 12:22
Variante pour 4) :

val. propre de A
V= (A.V)+V=\lambda V +V =(\lambda+1)V)
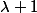
valeur propre de

Les v.p. de A étant

et

, celles de

sont

et

et

est inversible si

soit

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2015, 12:23
par Carpate » 04 Jan 2015, 12:23
trablazar a écrit:Ah oui je me rends compte que j'ai tout mélangé pour le coup...
Je ne savais pas par ou commencer, mais c'est vrai que poser

est le plus logique! Merci beaucoup !
Et surtout revois le théorème du rang ....
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 12:35
par trablazar » 04 Jan 2015, 12:35
Carpate a écrit:Variante pour 4) :

val. propre de A
V= (A.V)+V=\lambda V +V =(\lambda+1)V)
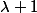
valeur propre de

Les v.p. de A étant

et

, celles de

sont

et

et

est inversible si

soit

Et cette méthode fonctionne uniquement avec I + A ou s'étend-elle pour toute matrice B ayant une seule valeur propre ?
Pour ce qui est du théorème du rang, c'est vrai que l'a c'etait pas joli, mais c'est noté, ca devrait pas se reproduire!
Par ailleurs, que penses-tu de mon deuxieme commentaire, concernant la 6) ?
Merci beaucoup en tout cas!
-
Eogel
- Messages: 4
- Enregistré le: 04 Jan 2015, 11:38
-
 par Eogel » 04 Jan 2015, 15:36
par Eogel » 04 Jan 2015, 15:36
trablazar a écrit:Et cette méthode fonctionne uniquement avec I + A ou s'étend-elle pour toute matrice B ayant une seule valeur propre ?
Y'a un résultat qui dit que si A et B sont semblables, alors A + aIn semblable à B + aIn (en fait c'est même P(A) semblable à P(B) où P est un polynome).
(Donc ici A a comme valeur propre 0 et alpha. Donc A est semblable à une matrice diagonale avec des 0 et des alpha sur la diagonale. Donc A+In est semblable à cette matrice diagonale + In, et donc les valeurs propres de A+In sont bien (les valeurs propres de A) + 1)
Cela ne dépend pas du nombre de valeurs propres!
Je sais pas si j'ai répondu à ta question :p
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 16:13
par trablazar » 04 Jan 2015, 16:13
Eogel a écrit:Y'a un résultat qui dit que si A et B sont semblables, alors A + aIn semblable à B + aIn (en fait c'est même P(A) semblable à P(B) où P est un polynome).
(Donc ici A a comme valeur propre 0 et alpha. Donc A est semblable à une matrice diagonale avec des 0 et des alpha sur la diagonale. Donc A+In est semblable à cette matrice diagonale + In, et donc les valeurs propres de A+In sont bien (les valeurs propres de A) + 1)
Cela ne dépend pas du nombre de valeurs propres!
Je sais pas si j'ai répondu à ta question :p
Ouaip c'est compris ! Je partais pas dans le bon sens mais je m'attendais à un truc comme ca ^^
Au passage tu as une idée de comment faire pour la 6) ? J'ai commencé a à répondre dans mon deuxieme commentaire, mais je bute un peu la :mur:
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 04 Jan 2015, 20:11
par trablazar » 04 Jan 2015, 20:11
Personne n'a d'idée pour la 6) ? :ptdr:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Jan 2015, 14:31
par Carpate » 05 Jan 2015, 14:31
Du coup pour la 6) Je fais :
b = V^T M^{-1} U
b V^T = V^T M^{-1} A J'additionne par V^T des deux cotés
V^T (b+1) = V^T (I + M^{-1} A) Donc si b = -1, I + M^{-1} A = 0 donc non inversible car 0 est
A partir de ton expression :
V^T = V^T (I + M^{-1} A))
Recherche des val. propres :

et vecteurs propres

de

:
 X= \mu X)
 X= \mu V^TX)
V^T.X = \mu V^TX)
Identité si


valeur propre de

qui est inversible pour
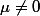
soit

Qui fera la 6-b) ?
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 05 Jan 2015, 19:26
par trablazar » 05 Jan 2015, 19:26
Carpate a écrit:A partir de ton expression :
V^T = V^T (I + M^{-1} A))
Recherche des val. propres :

et vecteurs propres

de

:
 X= \mu X)
 X= \mu V^TX)
V^T.X = \mu V^TX)
Identité si


valeur propre de

qui est inversible pour
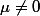
soit

Qui fera la 6-b) ?
Ah oui en effet, je pensais pas qu'il fallait juste l'identité!
Pour la 6)b), il y a surement du
 = M + A)
par exemple:
M est inversible (énoncé) et

est inversible.
Or,
) = det (I + M^{-1} A) * det (M)) ET
ET  \neq 0)
et

DONC
) \neq 0)
donc inversible
C'est bon ?
Je vais chercher pour 6)c) maintenant!
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 05 Jan 2015, 19:45
par trablazar » 05 Jan 2015, 19:45
Pour la c), je pars de:
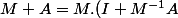)
^{-1} = (I + M^{-1} A)^{-1} . M^{-1})
Je suis sensé aller plus loin ? Je ne sais rien de M
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Jan 2015, 20:49
par Carpate » 05 Jan 2015, 20:49
trablazar a écrit:Ah oui en effet, je pensais pas qu'il fallait juste l'identité!
Pour la 6)b), il y a surement du
 = M + A)
par exemple:
M est inversible (énoncé) et

est inversible.
Or,
) = det (I + M^{-1} A) * det (M)) ET
ET  \neq 0)
et

DONC
) \neq 0)
donc inversible
C'est bon ?
Je vais chercher pour 6)c) maintenant!
Y'a plus simple :
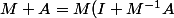)

est inversible par hypothèse,

est inversible si (c.n.s.) b
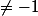
Le produit de 2 matrices inversibles est (une matrice) inversible et leur produit est le produit des matrices inverses (pris dans l'ordre inversé) :

est une condition nécessaire et suffisante pour que (M + A) soit inversible et son inverse est :
^{-1}=(I+M^{-1} A)^{-1}. M^{-1})
-
trablazar
- Membre Relatif
- Messages: 111
- Enregistré le: 29 Déc 2011, 11:05
-
 par trablazar » 05 Jan 2015, 20:54
par trablazar » 05 Jan 2015, 20:54
Carpate a écrit:Y'a plus simple :
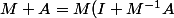)

est inversible par hypothèse,

est inversible si (c.n.s.) b
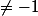
Le produit de 2 matrices inversibles est (une matrice) inversible et leur produit est le produit des matrices inverses (pris dans l'ordre inversé) :

est une condition nécessaire et suffisante pour que (M + A) soit inversible et son inverse est :
^{-1}=(I+M^{-1} A)^{-1}. M^{-1})
Ok ok bah du coup c'est terminé !!! Merci à toi Carpate et merci à tous les autres qui m'ont aidé! Bonne soirée !!! :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
