Bonjour j'aimerais bien avoir une aide sur ce QCM qu'il faut justifier
1/ le système d'équations x-y=2
x-y=0
a) n'a aucune solution
b) a un seul couple de solution
c) a une infinité de couples solutions
2/ on admet que le système d'équations 2x+3y=-7
X-4=13 a un seul couple de solution
a) (3;-1). b) (1;-3). c) (1;3).
en justifiant s'il vous plait, merci!
Équations de droite
11 messages
- Page 1 sur 1
Britanny a écrit:Bonjour j'aimerais bien avoir une aide sur ce QCM qu'il faut justifier
1/ le système d'équations x-y=2
x-y=0
a) n'a aucune solution
b) a un seul couple de solution
c) a une infinité de couples solutions
2/ on admet que le système d'équations 2x+3y=-7
X-4=13 a un seul couple de solution
a) (3;-1). b) (1;-3). c) (1;3).
en justifiant s'il vous plait, merci!
Merci Britanny pour tes compliments qui me touchent, je n'ai que 5 minutes, je te réponds vite fait, désolé :
1) transformation : équation sous forme de système ===> équation réduite (permet de tracer la droite rapidement mais surtout de visualiser sa pente avec le a de y=ax+b)
x-y=2 =====> y=x-2 ===> y=1x-2
y-x=0 =====> y=x ===> y=1x
trace les droites, mais même sans les tracer tu constate qu'elles sont // puisque leur coeff directeur =1 pour chacune donc elles ne se coupent pas donc S = ensemble vide
et par le calcul on arrive à 0y=-2 donc pas de solution ! (donc calcul et graphe sont cohérents ! = tout va bien)
2)
je trouve b) (1;-3) -------->attention tu as écrit x-4=13 au lieu de x-4y=13
graphiquement les droites se coupent en x= 1 et y=-3 (pour justifier tu peux faire le calcul et / ou le graphe)
Bonne journée ! et merci Britanny !
Britanny a écrit:Laetidom: merci beaucoup à vous, donc lorsqu'elles sont parallèles il n'y a aucune solution?
Signer: oui je me suis trompée pardon c'est x-4y=13
Moi j'ai trouvée b)
Si des droites sont // tu n'a donc pas de solution commune !, graphiquement ça devient évident ! (// donc pas de point d'intersection donc pas de solution) puisque tu cherche la solution DU système, donc du système composé des 2 droites ! Comprends-tu ?....
Bonne journée à tous ! ! !
Re-bonjour Britanny,
je reviens juste et découvre ton gentil message :
par le calcul :
1) 2x+3y=-7
2) x-4y=13
de la 2) : x=13+4y que je remets dans la 1)
ça donne : 2(13+4y) +3y=-7
26+8y+3y=-7
11y=-7-26=-33
d'où y=-3 que tu mets dans la 2) par exemple :
x-4.(-3)=13
x=13-12=1
x=1
d'où S={1 ; -3}
-----------------------------
et par le graphique ça donne la même chose S={1 ; -3} que tu peux voir sur le lien ci-après :

-----------------------------
Si tu trace tes droites à la main ou que tu les saisisse sur ta calculatrice graphique il est peut-être plus judicieux d'utiliser l'équation réduite y=ax+b, moi j'ai utilisé Geogebra qui est hyper facile d'utilisation (équation réduite ou pas, le logiciel traite sans problème !!!) Bonne journée et bonne lecture !
------------------------------------
1) y= -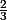 x -
x - 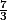
2) y=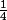 x -
x - 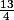
(-7/3) et (-13/4) ceux sont ce qu'on appelle les "ordonnées à l'origine". A l'origine de quoi ? et bien à l'origine des abscisses ! (que tu peux aisément contrôler visuellement sur le graphe)
et tu aura reconnu bien sûr que (-2/3) et (1/4) sont les coefficients directeurs [appelé aussi coefficient angulaire, c'est lui qui donne la pente (l'orientation, par rapport à l'ordonnée à l'origine, c'est-à-dire par rapport au point (0 ; b) avec b venant de y=ax+b) de la droite] des droites
sur le lien a correspond à 1) et b correspond à 2) et A correspond au point d'intersection des droites c'est-à-dire à la solution (1 ; -3) du système !
de plus, sur le lien tu peux remarquer que a descend car le coeff directeur = -2/3 = négatif !
et que b monte car le coeff directeur = +1/4 = positif !
je reviens juste et découvre ton gentil message :
par le calcul :
1) 2x+3y=-7
2) x-4y=13
de la 2) : x=13+4y que je remets dans la 1)
ça donne : 2(13+4y) +3y=-7
26+8y+3y=-7
11y=-7-26=-33
d'où y=-3 que tu mets dans la 2) par exemple :
x-4.(-3)=13
x=13-12=1
x=1
d'où S={1 ; -3}
-----------------------------
et par le graphique ça donne la même chose S={1 ; -3} que tu peux voir sur le lien ci-après :
-----------------------------
Si tu trace tes droites à la main ou que tu les saisisse sur ta calculatrice graphique il est peut-être plus judicieux d'utiliser l'équation réduite y=ax+b, moi j'ai utilisé Geogebra qui est hyper facile d'utilisation (équation réduite ou pas, le logiciel traite sans problème !!!) Bonne journée et bonne lecture !
------------------------------------
1) y= -
2) y=
(-7/3) et (-13/4) ceux sont ce qu'on appelle les "ordonnées à l'origine". A l'origine de quoi ? et bien à l'origine des abscisses ! (que tu peux aisément contrôler visuellement sur le graphe)
et tu aura reconnu bien sûr que (-2/3) et (1/4) sont les coefficients directeurs [appelé aussi coefficient angulaire, c'est lui qui donne la pente (l'orientation, par rapport à l'ordonnée à l'origine, c'est-à-dire par rapport au point (0 ; b) avec b venant de y=ax+b) de la droite] des droites
sur le lien a correspond à 1) et b correspond à 2) et A correspond au point d'intersection des droites c'est-à-dire à la solution (1 ; -3) du système !
de plus, sur le lien tu peux remarquer que a descend car le coeff directeur = -2/3 = négatif !
et que b monte car le coeff directeur = +1/4 = positif !
laetidom a écrit:Re-bonjour Britanny,
je reviens juste et découvre ton gentil message :
par le calcul :
1) 2x+3y=-7
2) x-4y=13
de la 2) : x=13+4y que je remets dans la 1)
ça donne : 2(13+4y) +3y=-7
26+8y+3y=-7
11y=-7-26=-33
d'où y=-3 que tu mets dans la 2) par exemple :
x-4.(-3)=13
x=13-12=1
x=1
d'où S={1 ; -3}
-----------------------------
et par le graphique ça donne la même chose S={1 ; -3} que tu peux voir sur le lien ci-après :
-----------------------------
Si tu trace tes droites à la main ou que tu les saisisse sur ta calculatrice graphique il est peut-être plus judicieux d'utiliser l'équation réduite y=ax+b, moi j'ai utilisé Geogebra qui est hyper facile d'utilisation (équation réduite ou pas, le logiciel traite sans problème !!!) Bonne journée et bonne lecture !
------------------------------------
1) y= -x -
2) y=x -
(-7/3) et (-13/4) ceux sont ce qu'on appelle les "ordonnées à l'origine". A l'origine de quoi ? et bien à l'origine des abscisses ! (que tu peux aisément contrôler visuellement sur le graphe)
et tu aura reconnu bien sûr que (-2/3) et (1/4) sont les coefficients directeurs [appelé aussi coefficient angulaire, c'est lui qui donne la pente (l'orientation, par rapport à l'ordonnée à l'origine, c'est-à-dire par rapport au point (0 ; b) avec b venant de y=ax+b) de la droite] des droites
sur le lien a correspond à 1) et b correspond à 2) et A correspond au point d'intersection des droites c'est-à-dire à la solution (1 ; -3) du système !
de plus, sur le lien tu peux remarquer que a descend car le coeff directeur = -2/3 = négatif !
et que b monte car le coeff directeur = +1/4 = positif !
Au risque de paraître debile, je ne comprends vraiment rien.. je suis désolée de vous déranger mais je n'arrive vraiment pas à refaire le graphique à la main!
Britanny a écrit:Au risque de paraître debile, je ne comprends vraiment rien.. je suis désolée de vous déranger mais je n'arrive vraiment pas à refaire le graphique à la main!
NON c'est moi qui suis désolé d'en avoir trop mis, je pensais que tu était ok.
Déjà comment fais-tu pour tracer la première droite (j'ai une méthode hyper simple et rapide, en "2 coups de crayon" si ça peut intéresser)
je t'explique pour faire le graphe à la main
Britanny a écrit:Au risque de paraître debile, je ne comprends vraiment rien.. je suis désolée de vous déranger mais je n'arrive vraiment pas à refaire le graphique à la main!
Je ne vais pas avoir beaucoup de temps alors je t'explique pour tracer la 1ère droite :
2x+3y=-7
en ce qui me concerne (d'autres te diront que non, chacun sa méthode) je trouve plus facile à tracer par l'équation réduite que voici :
y= -
je sais que la droite passe par (0 ; (-7/3)), tu es d'accord c'est l'ordonnée à l'origine
maintenant que j'ai un point voyons pour l'orientation : le coeff dir = -2/3
ce qui veut dire que si je trace depuis mon point connu (0 ; (-7/3)) un segment horizontal de longueur 1 vers la droite (positif) puis au bout de ce segment, un autre vertical vers le bas (car coeff négatif) de longueur (2/3) j'obtiens un second point : relis le point (0 ; (-7/3)) au second point et tu as ta pente donc ta droite !
--------------------------------------
Si tu trouve ma méthode compliquée :
tu as ton équation en x et y
tu prends arbitrairement x=0 et tu obtiens par l'équation un y ===> tu as 1 point
tu prends arbitrairement x=3 et tu obtiens par l'équation un y ===> tu as 1 point
Trace la droite passant par les 2 points !
aide de lyne99 (pour calculer l'équation à partir de 2 points, toi c'est l'inverse) : http://dundee.pagesperso-orange.fr/maths/images/Image20.gif
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 152 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
