Suite majoree dure

[baridomerre]

Soit Un suite et n ;) 1
Un = ((1)/(1+n ))+((1)/(2+n))+………+((1)/(n+n))
Prouve que la suite est majoree par 3/4 3 quart quelque soit n ;) 1
merci d'avance

[masque gazé]

Salut

Instinctivement je dirais:

Un = ((1)/(1+n ))+((1)/(2+n))+………+((1)/(n+n)) =

donc Un

L'idée est donc de majorer ta suite. MA majoration n'est peut etre pas suffisante, je te laisse donc l'améliorer :lol3:

[baridomerre]

Merci a toi pour ton attention ja essaye avec cette idee mais toujours inferieur a 1

[Ericovitchi]

he oui mais elle est dure à améliorer.
on peut déjà dire que la somme est plus petite que n fois son terme le plus grand donc inférieure à n/(n+1) mais ça ne suffit pas à montrer qu'elle est plus petite que 3/4.
La récurrence non plus ne marche pas.
Sur Iles-maths http://www.ilemaths.net/forum-sujet-625267.html sur laquelle tu as également posté, quelqu'un a démontré que la suite était croissante et tendait vers ln 2 qui est plus petit que 3/4. Mais il a utilisé des outils que tu n'es pas censé connaître en 1 ième (des équivalents de la série harmonique).
une démonstration simple, niveau première reste donc à trouver.

[Ben314]

Salut,
Tu sais ce que c'est une intégrale ? (ça pourrait grandement servir ici...)

[baridomerre]

peut tu meclairire plus jai rien compris comment utiliser la somme pour faire dementrer quil est moin de 3/4

[baridomerre]

Ben314 nnnn aucun resultat

[Ericovitchi]

oui c'est une bonne idée, on doit pouvoir facilement majorer et minorer cette somme vu comme une somme d'aires de rectangles par l'aire de la fonction inverse. Et comme ces intégrales se calculent facilement on doit pouvoir trouver ln(2) sans trop de problèmes.

Mais il est en première Ben, alors Rieman ou les intégrales, c'est un peu prématuré pour lui sans doute ?

[Ben314]

A la limite, sinon, on peut tenter une petite "astuce" de "somations par paquets" :
Montrer que, pour tout on a
puis écrit que

[Ben314]

Autre méthode, un peu plus alambiquée, mais qui permet de majorer 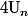avec autant de précision que l'on veut :
1) Vérifie que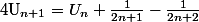
2) Déduit en que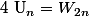 où
3) Montre que, si on pose alors est décroissante et que, pour tout ,
4) Bilan : n'importe quel terme constitue un majorant de la suite

EDIT : Tu peut même directement prendre et juste montrer que est décroissante, mais ça "sort un peu d'un chapeau".

[baridomerre]

EDIT : Tu peut même directement prendre et juste montrer que est décroissante, mais ça "sort un peu d'un chapeau".[/quote]

comment

[baridomerre]

merci de m'expliquer comment pruver que Vn est decroissante jarrive pas meme si jai suivi tous tes etapes

[baridomerre]

Ehooo comment utiliser laire de la fonction inverse