Bonsoir,
Pourriez vous m'aider à propos d'un exercice
Soit la fonction f définie sur R\4 par : f(x)= |2x-1|-|x-5|+|2x+4|
Résoudre par le calcul f(x) = -1. :hein:
voila ce que j'ai trouve :
f(x)=-1 => f(x)= |2x-1|-|x-5|+|2x+4| =-1
=|x+4|+|2x+4|
=|3x+8|
D'avance merci
Valeur absolue
5 messages
- Page 1 sur 1
Salut !
Reviens à la définition de la valeur absolue d'un réel :
:
[CENTER]
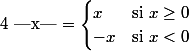 [/CENTER]
[/CENTER]
Par exemple :
[CENTER]
 & {\rm si}\ 2x-1<0 \end{cases} = \begin{cases} 2x-1 & {\rm si}\ x\ge \frac 1 2 \\ -(2x-1) & {\rm si}\ x<\frac 1 2 \end{cases}) [/CENTER]
[/CENTER]
Fais-en de même avec les autres termes de ta somme :++:
elvia.giannitelli a écrit:Bonsoir,
Pourriez vous m'aider à propos d'un exercice
Soit la fonction f définie sur R\4 par : f(x)= |2x-1|-|x-5|+|2x+4|
Résoudre par le calcul f(x) = -1. :hein:
voila ce que j'ai trouve :
f(x)=-1 => f(x)= |2x-1|-|x-5|+|2x+4| =-1
=|x+4|+|2x+4|
=|3x+8|
D'avance merci
Reviens à la définition de la valeur absolue d'un réel
[CENTER]
Par exemple :
[CENTER]
Fais-en de même avec les autres termes de ta somme :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

