Géometrie differentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par jesuisnulmaisjemesoigne » 23 Nov 2014, 12:05
par jesuisnulmaisjemesoigne » 23 Nov 2014, 12:05
Bonjour à tous,
Je viens de reprendre mes études, et c'est vraiment pas facile de s'y remettre.
Je travaille actuellement sur la géométrie différentielle et je rencontre pas mal de difficulté sur mon premier exercice notamment pour déterminer la normale principale et la courbure au point courant de cette courbe

je trouve comme vecteur unitaire tangent

donc il faut que je calcule la dérivée du vecteur tangent c'est bien ca ? ca peut paraitre nulle mais j'ai du mal a partir (peut être le dimanche matin qui me réussi pas)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 13:36
par Ben314 » 23 Nov 2014, 13:36
Salut,
Il est bizarre ton
vecteur (unitaire tangent) : on dirait bien que ce n'est pas un
vecteur mais un
scalaire...
Aprés, à mon avis, si tu veut pas trop te faire c..., tu introduit le vecteur
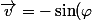\vec{\imath}+\cos(\varphi)\vec{\jmath})
:
La base (mobile)
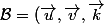)
est orthonormée directe et, pour les calculs de dérivée, tu as

et

.
Par exemple
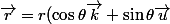\ \rightarrow\ (r\sin\theta\,,\,0\,,\,r\cos\theta)\)
dans

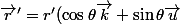+r\sin\theta\varphi'\vec{v}\ \rightarrow\ (r'\sin\theta\,,\, r\sin\theta\varphi'\,,\, r'\cos\theta)\)
dans

etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 13:57
par Ben314 » 23 Nov 2014, 13:57
Salut,
Il est bizarre ton
vecteur (unitaire tangent) : on dirait bien que ce n'est pas un
vecteur mais un
scalaire...
Aprés, à mon avis, si tu veut pas trop te faire c..., tu pose
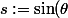)
,
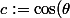)
(c'est des constantes) et tu introduit le vecteur
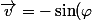\vec{\imath}+\cos(\varphi)\vec{\jmath})
:
La base (mobile)
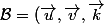)
est orthonormée directe et tu as

et

.
Par exemple
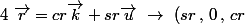\)
dans

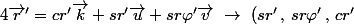\)
dans

etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 14:03
par Ben314 » 23 Nov 2014, 14:03
Salut,
Il est bizarre ton
vecteur (unitaire tangent) : on dirait bien que ce n'est pas un
vecteur mais un
scalaire...
Aprés, à mon avis, si tu veut pas trop te faire c..., tu pose
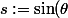)
,
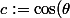)
(c'est des constantes) et tu introduit le vecteur
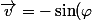\vec{\imath}+\cos(\varphi)\vec{\jmath})
:
La base (mobile)
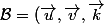)
est orthonormée directe et tu as

et

.
Par exemple
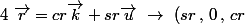\)
dans

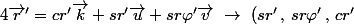\)
dans

etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités


