Équations différentielles

[faridrami]

Bonsoir :

S'il vous plait, je voudrais la solution particulière de cette équation différentielle du premier ordre et du deuxième degré : y² + (y')² = 1

dans la première étape on sait que cos²x+sin²x=1,alors après la simplification notre équation aura été: y+y'=cosx+sinx mais je ne peux pas résoudre cette dernière :help: .

cordialement

[WillyCagnes]

bsr

tu poses y=Acos(x)
y'=-Asin(x)

y²+y'² =A²(cos(x)² + sin(x)²)=A² =1
A=1
A=-1

solution generale
tu poses
y=Acos(x) + Bsin(x)
y'=-Asin(x) +Bcos(x)

te laisse calculer
y²+y'²=?

avec A²+B²=1 donc A se deduira en fonction de B

[mrif]

Bonsoir :

S'il vous plait, je voudrais la solution particulière de cette équation différentielle du premier ordre et du deuxième degré : y² + (y')² = 1

dans la première étape on sait que cos²x+sin²x=1,alors après la simplification notre équation aura été: y+y'=cosx+sinx mais je ne peux pas résoudre cette dernière :help: .

cordialement

Essaie de transcrire l'énoncé correctement.

[Ben314]

J'ai pas trop super bien compris l'énoncé, en particulier ça :

dans la première étape on sait que cos²x+sin²x=1,alors après la simplification ???? notre équation aura été: y+y'=cosx+sinx

Je ne comprend pas trop non plus ce qui permet à WillyCagnes de supposer que y=A.cos(t), voire y=A.cos(t)+B.sin(t) avec A et B constant (ou alors c'est juste pour trouver une solution particulière, mais comme on en as déjà une qui est triviale...)

Perso, j'aurais (bêtement) récrit l'équation sous la forme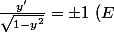 puis cherché une primitive de pour intégrer les deux membres de .

P.S. J'ai peut être mal compris la méthode de WillyCagnes : les A et les B peuvent représenter des fonctions (c'est l'équivalent de ce qu'on fait quand on utilise la méthode de variation de la constante dans des équation d'ordre 2...)
Mais dans ce cas, l'équation A²+B²=1 est à compléter avec l'autre équation sous-jacente au deux posées au départ...

[Ben314]

En fait, après calculs, c'est un peu pourri comme équa-diff :
On a comme solutions mézossi et on peut "recoller" les deux types de solutions en restant parfaitement .