DM complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
math41
- Messages: 4
- Enregistré le: 28 Oct 2014, 19:07
-
 par math41 » 28 Oct 2014, 19:19
par math41 » 28 Oct 2014, 19:19
Bonjour,
J'ai un exercice de mon devoir maison de Maths que je n'ai pas compris.
Exercice 1:
On donne z = 1+cos (alpha) + i sin (alpha), où alpha appartient à [0;pi].
1) En remarquant que alpha=2*(alpha/2) puis en utilisant les formules cos2(theta)=2cos²(theta)-1 et sin2(theta)=2sin(theta) cos(theta), simplifier l'écriture de z.
2) En déduire le module et l'argument de z. Justifiez soigneusement.
Pour la question 1), j'ai fait ça :
z=1+cos (alpha) + i sin (alpha)
z=1+cos(2alpha/2) + i sin (2alpha/2)
z=2cos²(alpha/2) + 2 i sin (alpha/2) cos (alpha/2)
Ensuite, je suis bloqué...
Si vous pourriez m'aider
Merci d'avance.
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 28 Oct 2014, 19:36
par gigamesh » 28 Oct 2014, 19:36
Tu as presque fini !
Mets 2 cos(alpha/2) en facteur.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Oct 2014, 19:37
par zygomatique » 28 Oct 2014, 19:37
salut
l'alphabet français compte 26 largement suffisantes pour se passer de l'alphabet grec .... :cry: :mur:
pour finir il suffit de factoriser ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 28 Oct 2014, 20:09
par mathelot » 28 Oct 2014, 20:09
z = 1+cos (alpha) + i sin (alpha)
z= 2cos(alpha:2)(au carré) + 2i sin(alpha:2)cos(alpha:2)
z= 2cos(alpha:2) (cos(alpha:2) + i sin(alpha:2))
z=2 cos(alpha:2) exp(i alpha:2)
-
mathelot
 par mathelot » 28 Oct 2014, 20:14
par mathelot » 28 Oct 2014, 20:14
zygomatique a écrit:salut
l'alphabet français compte 26 largement suffisantes pour se passer de l'alphabet grec ....

:mur:
pour finir il suffit de factoriser ...
ce n'est pas l'alphabet français, c'est l'alphabet latin (ou romain)
ici

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Oct 2014, 20:29
par zygomatique » 28 Oct 2014, 20:29
mathelot a écrit:z = 1+cos (alpha) + i sin (alpha)
z= 2cos(alpha:2)(au carré) + 2i sin(alpha:2)cos(alpha:2)
z= 2cos(alpha:2) (cos(alpha:2) + i sin(alpha:2))
z=2 cos(alpha:2) exp(i alpha:2)

:mur:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 28 Oct 2014, 21:32
par Carpate » 28 Oct 2014, 21:32
message supprimé
-
math41
- Messages: 4
- Enregistré le: 28 Oct 2014, 19:07
-
 par math41 » 28 Oct 2014, 21:47
par math41 » 28 Oct 2014, 21:47
Merci pour vos réponses.
Et pour la 2ème question:
module : |z|=racine(a²+b²)=racine((2cos(alpha)/2)²+(alpha/2)²)
Et argument = ??
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 28 Oct 2014, 21:52
par Carpate » 28 Oct 2014, 21:52
math41 a écrit:Merci pour vos réponses.
Et pour la 2ème question:
module : |z|=racine(a²+b²)=racine((2cos(alpha)/2)²+(alpha/2)²)
Et argument = ??
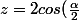 (cos(\frac{\alpha}{2})+isin(\frac{\alpha}{2})))
)
est un réel
+isin(\frac{\alpha}{2}))
est le complexe de module

et d'argument
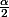
Donc le module de z est ... et son argument est ...
-
math41
- Messages: 4
- Enregistré le: 28 Oct 2014, 19:07
-
 par math41 » 28 Oct 2014, 21:58
par math41 » 28 Oct 2014, 21:58
Donc le module de z est 2cos(alpha/2) et son argument est (alpha/2).
C'est bien ça ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 28 Oct 2014, 22:01
par Carpate » 28 Oct 2014, 22:01
math41 a écrit:Donc le module de z est 2cos(alpha/2) et son argument est (alpha/2).
C'est bien ça ?
oui
cours :
le module d'un produit de complexes est le produit des modules de ces complexes
l'argument d'un produit de complexes est la somme des arguments de ces complexes (ici

et
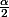
)
-
math41
- Messages: 4
- Enregistré le: 28 Oct 2014, 19:07
-
 par math41 » 28 Oct 2014, 22:18
par math41 » 28 Oct 2014, 22:18
D'accord. Merci à vous pour vos réponses.
-
mathelot
 par mathelot » 28 Oct 2014, 22:25
par mathelot » 28 Oct 2014, 22:25
math41 a écrit:Donc le module de z est 2cos(alpha/2) et son argument est (alpha/2).
C'est bien ça ?
Le module est toujours positif, le cosinus est positif selon les valeurs de alpha.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 132 invités
:mur:
