Bonjour à tous.
Alors voilà déjà 1 semaine que je gratte et que je rempli ma poubelle de feuilles remplies d'équation triturées dans tous les sens :mur: . Je suis perdu, c'est pourquoi je viens vers vous afin de trouver de l'aide.
Merci d'avance. :we:
Le problème est le suivant :
Calculer I1 et I2
A l'aide de ces équations :
E1 - I1r1 = V = I2R
E2 - (I2-I1)r2 = V = I2R
J'ai le schéma s'il peut aider, mais je ne vois pas comment poster une image dans un topic.
Mais je n'ai aucune valeurs de résistance ni de tension.
J'imagine bien que je dois obtenir un rapport mais je n'arrive pas à simplifier et réduire les équations suffisamment.
Respectueusement
Veknar.
Elec & maths (équations)
7 messages
- Page 1 sur 1
Veknar a écrit:Bonjour à tous.
Alors voilà déjà 1 semaine que je gratte et que je rempli ma poubelle de feuilles remplies d'équation triturées dans tous les sens :mur: . Je suis perdu, c'est pourquoi je viens vers vous afin de trouver de l'aide.
Merci d'avance. :we:
Le problème est le suivant :
Calculer I1 et I2
A l'aide de ces équations :
E1 - I1r1 = V = I2R
E2 - (I2-I1)r2 = V = I2R
J'ai le schéma s'il peut aider, mais je ne vois pas comment poster une image dans un topic.
Mais je n'ai aucune valeurs de résistance ni de tension.
J'imagine bien que je dois obtenir un rapport mais je n'arrive pas à simplifier et réduire les équations suffisamment.
Respectueusement
Veknar.
On checrche
Essaie de transformer le système de départ:
de façon à aboutir à un système de la forme:
qui est facile à résoudre.
Essaie, ça ne présente aucune difficulté.
mrif a écrit:On checrcheet tout le reste est connu sauf V qu'on déduira.
Essaie de transformer le système de départ:
de façon à aboutir à un système de la forme:
qui est facile à résoudre.
Essaie, ça ne présente aucune difficulté.
Alors voilà j'ai aisément obtenu le système que tu me proposais.
J'obtiens donc :
1)
2 )
Ensuite j'ai essayé de réaliser :
-> 2)/1) (Cela supprime mes
Donc à mon sens pas intéressant.
-> 1)-2) (je peux obtenir soit
Mais je ne pense pas que ces résultats soient satisfaisant... :hum:
Veknar a écrit:Alors voilà j'ai aisément obtenu le système que tu me proposais.
J'obtiens donc :
1)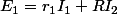
2 )
Ensuite j'ai essayé de réaliser :
-> 2)/1) (Cela supprime meset
)
Donc à mon sens pas intéressant.
-> 1)-2) (je peux obtenir soit= soit
=
Mais je ne pense pas que ces résultats soient satisfaisant... :hum:
Le nouveau système que tu as trouvé est correct.
Pour le résoudre tu peux procéder comme ceci:
Tu multiplie les 2 membres de l'équation (1) par
mrif a écrit:Le nouveau système que tu as trouvé est correct.
Pour le résoudre tu peux procéder comme ceci:
Tu multiplie les 2 membres de l'équation (1) paret ceux de l'équation (2) par
, ensuite tu additionnes membre à membre les 2 équations obtenues et tu en déduis
puis en remplaçant la valeur obtenue de
dans l'une des 2 équations de départ tu en déduiras
.
Ok alors voilà ce que j'obtiens. Et c'est à mon sens pas du tout satisfaisant
1)
2)
1)+2) -->
Je ne vois pas comment réduire d'avantage. Et ensuite par substitution j'essaie de faire :
Et là je tombe sur une équation chargée.
Ça sent pas bon cette histoire ^^ :mur:
J'essai en suivant vos conseils mais je tombe sur un mur à chaque marche
WillyCagnes a écrit:Bjr
tu as bien trouvé 1) et 2)
L' ADDITION 1+2 donne:
avec R1R2I1 qui s'elimine
(E1.R2 +E2.R1)=I2(R.R2+R+R2+R1)
d'où
I2= (E1.R2 +E2.R1)/(R.R2+R+R2+R1) tout simplement
te laisse continuer pour trouver I1 avec 1) ou la 2)
il fallait bien suivre les conseils de Mrif
Merci c'est vrai j'ai foiré la simplification ^^
Pour
Qu'en dîtes vous ?
Peut-on considérer l'équation résolue ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
