Combinatoire

[Al-Kashi]

Bonjour,
J'ai essayé de faire cet exercice mais j'y arrive pas.
---------------------------------------------------
On a placé un jeton sur chaque sommet d’un polygone régulier à 1997 côtés. Sur chacun de ces jetons est inscrit un entier relatif, la somme de ces entiers relatifs étant égale à 1. On choisit un sommet de départ et on parcourt le polygone dans le sens trigonométrique en ramassant les jetons au fur et à mesure tant que la somme des entiers inscrits sur les jetons ramassés est strictement positive.
Peut-on choisir le sommet de départ de façon à ramasser tous les jetons ? Si oui, combien y-a-t-il de choix
possibles ?

[Doraki]

Il me semble qu'il y a toujours un seul choix possible, non ?

[chan79]

Si on considère un pentagone, en disposant dans le sens positif: -2, 3, 4, 4 et -8, on peut partir du -2 et aussi du 3.

[Doraki]

Ben non si on part de -2 on ramasse -2 et on s'arrête immédiatement puisque -2 <= 0

[beagle]

Si on considère un pentagone, en disposant dans le sens positif: -2, 3, 4, 4 et -8, on peut partir du -2 et aussi du 3.

Bien vu Chan,
j'ai juste joué avec ce problème 5 mn ce matin et je restais à 1 comme l'indiquait Doraki.
les structures type:
-1 + 2 + 2 - 2 fonctionnent à 2
comme les
-a + (a+1) +[...] un truc qui s'annule et respecte l'énoncé

quelles autres structures fonctionnent?

[cuati]

Bonjour,

Unicité :
Si deux tels sommets et existent alors la somme du premier sommet jusqu'à celui juste avant le second sommet serait strictement positive (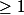 pour des entiers) et la somme du second jusqu'à celui avant le premier serait aussi strictement positive ( 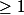pour des entiers). Donc le total devrait au moins être égal à 2, ce qui n'est pas.

Existence (vaut mieux faire un dessin) : avec sommets.
Supposons qu'aucun des sommets de départ ne fonctionnent.
Alors on en prend un au hasard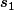 et on commence à parcourir le polygone et on s'arrête quand la comme est négative ou nulle. Puis on recommence en partant du sommet suivant jusqu'à ce que la somme soit à nouveau négative ou nulle.
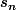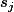De cette manière on va essayer de partitionner les sommets en sommets consécutifs de sommes négatives ou nulles : Le seul problème qui se pose est au moment où on revient sur le sommet de départ. Il faut alors remarquer que si la dernière somme ne s'arrête pas à alors cela signifie que et donc la somme commençant à s'arrête nécessairement à l'un des car si elle s'arrête à avec et par définition de , ce qui est absurde. On peut donc regrouper la dernière partie de la partition avec certaines des premières parties pour au final avoir une vraie partition de tous les sommets en sommets de sommes négatives ou nulles, ce qui est impossible d'après l'énoncé, puisque le total doit faire 1.

[nodjim]

J'avais déja eu à réfléchir à cette question et je la résolvais en groupant la somme des valeurs successives en + ou - selon la valeur moyenne, et ensuite en disant qu'en regroupant un +-, si le résultat était +, alors la somme des valeurs successives était forcément +.

[zygomatique]

salut

il me semble que pour l'existence il suffit de dire ::


pour tout sommet au hasard que je numérote 1 je considère la somme où p est le plus grand entier tel que pour tout k entre 1 et p S(k) > 0 et S(p + 1) =< 0

si pour tout sommet initial p ne prend jamais la valeur 1997 alors cela contredit l'hypothèse que la somme totale des sommets est 1

[Al-Kashi]

Bonjour,

Je vous remercie pour vos réponses. J'ai trouvé une solution mais il me semble que la conclusion sur l'unicité est discutable.

[mathelot]

Il me semble qu'il y a un seul choix possible, non ?

je n'ai pas trop compris si tu avais une démonstration

[mathelot]

Bonjour,

Je vous remercie pour vos réponses. J'ai trouvé une solution mais il me semble que la conclusion sur l'unicité est discutable.

je l'avais pas trouvée :ptdr:

t'as quoi comme moteur de recherche ?