Géométrie espace

[pashan66]

Bonjour

Voici un exercice de géométrie de l'espace sur lequel je butte.

Enoncé

On donne le cube ABCD A'B'C'D' d'arête a et P le point milieu de [A'B']
a) démontrer que le triangle PB'C est rectangle
b) calculer l'amplitude de l'angle APC
c) calculer l'aire de triangle APC

merci

[Ericovitchi]

la a) est facile, PB' est perpendiculaire au plan BCC'B' donc à toute droite du plan dont B'C.
b) grâce au triangle PB'C tu peux trouver PC avec Pythagore (tu as facilement les deux autres cotés) , tu peux aussi calculer AD et AC. Tu auras l'angle en utilisant le théorème d'Al-Kashi.

[pashan66]

Merci Ericovitchi

En suivant tes précieux conseils je trouve pour
AP = a/2. ( racine de 5)
AC = a . (racine de 2)
PC = 3/2 a

en développant la formule de Al Kashi je trouve un angle de 68° (est-ce correct?)

Pour l'aire du triangle j'applique la formule (b*h)/2 avec b = AC mais que vaut h?

Est il possible d'utiliser la formule générale suivante
S = 1/2. b. c . sin A

soit S = 1/2. AP . PC . Sin 68°

merci

[chan79]

Merci Ericovitchi

En suivant tes précieux conseils je trouve pour
AP = a/2. ( racine de 5)
AC = a . (racine de 2)
PC = 3/2 a

en développant la formule de Al Kashi je trouve un angle de 68° (est-ce correct?)

salut
entre 63° et 64° je pense

[paquito]

Quand tu travaille avec un cube, tu peut toujours supposer que le côté vaut 1 (quitte à multiplier toutes les longueurs par a ensuite); ton cube te permet alors de définir un repère orthonormé direct de l'espace et d'avoir des calculs simplifiés. ici, le repère qui s'impose est:
R=(D;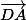 , , 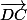); dans ce repère (je passe sur la première question), tu as A(1; 0; 0); C(0; 1; 0) et P(1;1/2;1) d'où (-1; 1; 0) ,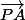 (0; -1/2; -1) puis (-1; 1/2; -1); tu en déduis 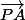.=3/4, puis AC= , PA=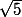/2 et PC=3/2. Tu peut appliquer Cos()==(3/4)/(3V5/4)=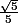, ce qui me donne Cos()=63,43°. Normalement, je devrais trouver la même chose que toi???
La métode n'est pas très élégante, mais elle est facile à appliquer. Pour l'aire tu as la bonne formule.

[chan79]

Merci Ericovitchi



Pour l'aire du triangle j'applique la formule (b*h)/2 avec b = AC mais que vaut h?


merci

Calcule plutôt la hauteur issue de A (elle vaut 1)

[Ericovitchi]

Pour l'aire, tu as les 3 cotés donc tu peux aussi utiliser la formule de Heron A=racine(p(p-a)(p-b)(p-c)) avec p=(a+b+c)/2

[paquito]

Pour l'aire, tu as les 3 cotés donc tu peux aussi utiliser la formule de Heron A=racine(p(p-a)(p-b)(p-c)) avec p=(a+b+c)/2

, le calcul est immédiat; on obtient 3a²/4 tout comme en passant par la hauteur issue de A (mais il faut la trouver), la formule de Héron est efficace, mais je ne pense pas qu'elle fasse partie du programme.