Exo Résolu : géométrie dans l'espace

[haricot29]

Voila j'ai un exercice a faie j'aimerais savoir si ce que j'ai fait est correct, merci à ceux qui prendrons le temps de regarder... Bonne journée a tous

Soient a un réel strictement positif et OABC un tétraèdre tel que :
OAB, OAC et OBC sont des triangles rectangles en O.
OA = OB = OC = a.

On appelle I le pied de la hauteur issue de C du triangle ABC, H le pied de la hauteur issue de O du triangle OIC, et D le point de l'espace défini par vecteur HO = vecteur OD.

1. Quelle est la nature du triangle ABC ?

2. Démontrer que les droites (OH) et (AB) sont orthogonales, puis que H est l'orthocentre du triangle ABC.

3. Calcul de OH.
a. Calculer le volume V du tétraèdre OABC puis l'aire S du triangle ABC.
b. Exprimer OH en fonction de V et de S, en déduire que OH= a * rac(3)/3.

4. Etude du tétraèdre ABCD.
L'espace est rapporté au repère orthonormal (o; 1/a vecteru OA ; 1/a vecteur OB ; 1/a vecteur OC).
a. Démontrer que le point H a pour coordonnées : (a/3 ; a/3 ; a/3).
b. Démontrer que le tétraèdre ABCD est régulier (c'est-à-dire que toutes ses arêtes ont même longueur).
c. Soit W le centre de la sphère circonscrite au tétraèdre ABCD.
Démontrer que W est un point de la droite (OH) puis calculer ses coordonnées.

Questions répondues

[Lierre Aeripz]

Montre nous ce que tu as fais, sinon on ne peut pas te dire si tu as bon...

[haricot29]

1) Les triangles OAB, OAC, OBC sont des triangles rectangles en O.Ils sont donc tous un angle égal à savoir l'angle droit en O.
De plus OA=OB=OC soit OAB, OAC et OBC sont isométriques puisqu'ils ont leurs côtés égaux deux à deux .
Soit : AB=AC=BC.
D'ou le traingle ABC est un triangle équilatéral.

2) On calcul le produit scalaire : ( ici tout en vecteur)
OH * AB = (OI+IH) AB = OI AB + IH AB
OI AB = 0 car (OI) est la hauteur issue de O.
IH AB = 0 car " oups la je ne vois pas comment dire "

donc OH AB = 0 Lesdroites (OH) et (AB) sont perpendiculaires.

[Lierre Aeripz]

Tout est bon !
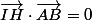
car (CI) est la hauteur issue de C de ABC, et que !

[haricot29]

2) suite (modifications)
si H est l'orthocentre de ABc alors (en vecteur) AH BC=0
vérifions : ( en vecteur)
AH BC = (AO +OH) BC = AO BC + OH BC
AO BC = 0 car (AO) perpendiculaire à (OBC)
OH BC = 0 car (OH) perpendiculaire à (ABC)
Donc AH BC = 0
Comme (AH) perpendiculaure à (BC) alr (AH) hauteur issue de A dans ABC
H étant intesection des hauteurs (CI) et (AH) H est l'orthocentre de ABC

[haricot29]

je reviens en fin de soirée...

[haricot29]

quelq'un peut il me confirmer pour la 2) et si possible m'éclairer, je reviens plus tard

[haricot29]

quelq'un peut il me confirmer pour la 2) et si possible m'éclairer sur ce qui est en gras , je reviens plus tard...
Meric d'avance :id:

[haricot29]

3)a) volume du tétraède ABCO
V = 1/3 *aire base*hauteur

On pren ABO comme base
aire de la base = 1/2*OA*OB= a²/2

V= 1/3* a²/2 * OC = a^3 / 6

aire du triangle ABC
S= 1/2 *AB*Ic = 1/2 * arac(2)*AC*cos(pi/6)
S= = (a²rac(3))/2

3)b)
On prend ABC comme base le volume est alors
V = 1/3*aire base*hauteur
V= 1/3*S*OH
D'ou OH = 3V/S = a/rac(3) = (arac(3))/3 = a * rac(3)/3

C'est toujours ok jusque la ?!

[fonfon]

salut, je n'ai pas regardé la 2) mais la 3) c'est ok

[haricot29]

4)a) H est l'orthocentre du triangle ABC c'est aussi son centre de gravité :
On a A(a,0,0) b(0,a,0) et c(0,0,a)
donc H(a/3,a/3,a/3

[fonfon]

4)a) H est l'orthocentre du triangle ABC c'est aussi son centre de gravité :
On a A(a,0,0) b(0,a,0) et c(0,0,a)
donc H(a/3,a/3,a/3

oui, c'est bon

[haricot29]

merci, c'est bon j'ai bouclé mon exercice pour la fin c'est ok j'ai vérifié avec une amie !
Merci encore :++: :++: :++: :++:

[fonfon]

re, une piste pour montrer que le tétraèdre est régulier

le point D est le symétrique de H par rapport à O donc les coordonnées de D sont ....

[fonfon]

ah ben alors tant mieux si tu as fini ton exo

A+