Trigonométrie

[Caramath]

Bonjour,

Je suis en faculté de médecine et je voudrais résoudre le problème suivant :

Soit une corde autour de l'équateur.
Admettons que l'équateur fasse 40 000 000 mètres de long, et la corde 40 000 006.
Imaginons une fusée qui soulève un point S de la corde jusqu'à ce qu'elle se tende.
Quelle est alors l'altitude x du point S ?

En termes géométriques on a donc un cercle de périmètre 40 000 000, de centre O et de rayon r, et un triangle isocèle ABS.
A et B sont les points de l'équateur (du cercle) d'où la commence à "s'élever".
S est le point où la corde est la plus éloignée du cercle.
La somme des distances AS et SB (corde tendue) est donc égale à l'arc de cercle AB (portion de l'équateur non en contact avec la corde) + 6 mètres.

Mes calculs m'ont mené à tourner en rond avec de la trigonométrie sortie de ma mémoire :
x = (r(1-cos(AOS))/(cos(AOS)) où 2r tan(AOS) = 2*r(angles AOS) + 6
Mais je ne sais pas comment concilier variables trigonométriques avec variables non trigonométriques.

edit : J'ai obtenu une estimation grâce à un logiciel de géométrie mais le chemin mathématique me laisse perplexe.

[siger]

bonsoir,

les angles etant petits il suffit de confondre les angles et les sinus ( ou tangentes) en prenant les angles en radians et d'ecrire
sin(a) = tan(a) = a
cos(a) = 1-a^2/2

[Caramath]

Bonsoir,
Merci pour votre réponse, cependant, j'ai l'impression qu'elle ne mène pas à la solution.

En effet :
tan(a) = (ra+3)/r
sin(a) = (ra+3/(r+x)
Si tan(a) = sin(a), alors x = 0 et le problème tombe à l'eau.

D'autre part si je l'introduis dans mon équation pour calculer "a" :
rtan(a) = ra + 3
Cela nous donne :
ra = ra +3
0 = 3

Comment confondre angles et sinus dans ce contexte où l'altitude, bien que négligeable au regard du rayon, est non nulle ?

Pour indication, après estimation géométrique, x = environ 400 (pour r = 6 366 198 )

Merci,

[Ben314]

Salut,
Soit le rayon de ton cercle et 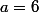la longueur "ajoutée".
Si on note l'angle AOS alors la longueur de l'arc AB du cercle est et la longueur des segments [AS] et [BS] est donc en fait ce qui signifie que l'angle est tel que .
L'altitude du point est alors .

Jusque là, c'est exactement ce que tu as écrit...

Le problème, c'est qu'on ne sait pas résoudre de façon exacte et avec les fonctions "élémentaires" une équation de la forme MAIS, comme la constante est très petite, est très proche de 0 et on peut effectivement utiliser le D.L. de pour évaluer la solution.
Évidement, pour qu'il reste quelque chose dans , il faut être plus précis que le simple et utiliser de façon à ce que l'équation devienne et donc .
Ensuite, en utilisant le fait que , on a

A.N.