Sinus

[vicchaix]

Bonjour,
est ce que j*sin(2*pi*f) est égale à j*sin(4*pi*f) ? (à deux pi près) ?
Merci beaucoup :id:

[Ben314]

Salut,
Est ce que sin(2x)=sin(x) ?

[vicchaix]

Merci de la réponse.
sin(2x)=sin(x) est faux mais lorsqu'il y a des "pi" sa change pas quelque chose ... ? :)

[vicchaix]

Merci de la réponse.
sin(2x)=sin(x) est faux mais lorsqu'il y a des "pi" sa change pas quelque chose ... ?

Donc la ligne que j'ai soulignée sur mon image ci dessous est fausse ?


merci !

[Ben314]

Merci de la réponse.
sin(2x)=sin(x) est faux mais lorsqu'il y a des "pi" sa change pas quelque chose ... ?

Ça dépend si ta variable f est entière ou pas : si elle est entière, alors les deux sinus sont nuls donc égauc.
Si elle n'est pas entière, alors tu pose x=2.pi.f qui est un réel totalement quelconque (si f était quelconque) et ce que tu as écrit, c'est précisément sin(x)=sin(2x) avec x quelconque...

Et comme tu n'as hélas pas précisé la nature des variables que tu écrivait ni quel statut elles avaient (est-ce un "pour tout f" ? "un pour tout j" ? ou bien j est il fixé ? peut-il être nul ?)
Donc aussi bien je répond comlétement à coté de la plaque...

P.S. Ton lien ne marche pas : tu n'as pas classé ton fichier en "public".

[vicchaix]

Ça dépend si ta variable f est entière ou pas : si elle est entière, alors les deux sinus sont nuls donc égauc.
Si elle n'est pas entière, alors tu pose x=2.pi.f qui est un réel totalement quelconque (si f était quelconque) et ce que tu as écrit, c'est précisément sin(x)=sin(2x) avec x quelconque...

Et comme tu n'as hélas pas précisé la nature des variables que tu écrivait ni quel statut elles avaient (est-ce un "pour tout f" ? "un pour tout j" ? ou bien j est il fixé ? peut-il être nul ?)
Donc aussi bien je répond comlétement à coté de la plaque...

P.S. Ton lien ne marche pas : tu n'as pas classé ton fichier en "public".

D'accord
Alors j est un complexe, et f la fréquence en physique.
Voilà l'image est public, pouvez vous jeter un oeil svp?
Sachant que l'énoncé est
Merci

[deltab]

Bonjour

Bonjour,
est ce que j*sin(2*pi*f) est égale à j*sin(4*pi*f) ? (à deux pi près) ?
Merci beaucoup :id:

Tu sembles confondre et
Compares les deux expressions pour

[vicchaix]

Merci pour vos réponses !
Oui je crois que je confond tous là ....
Alors seriez vous répondre à la question 1.1 de l'énoncé ?
Merci

[Ben314]

Je ne connais absolument rien au "traitement du signal".

J'aurais tendance à supposer que les fonctions Y(Z) et X(Z) sont les "fonctions génératrices" des suites et (sont_ce bien des suites ? sont elles effectivement définies pour 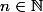ou serait-ce pour ?) ç'est ça :
et

Mais je préfèrerais avoir confirmation avant de me lancer dans les calculs...