Produit Scalaire

[pbongrand]

bonjour a tous, je suis face à un exercice qui me pose beaucoup de problèmes.... je pense avoir compris la question posée mais je ne sais pas par ou commencer....

énoncé:

Dans un repère orthonormé, on donne les points ;)(0 ; 2), ;)(;)1 ; 1) et ;)(4 ; 0).
Calculer au dixième près la mesure de l’angle ;););).

Idées:

J'ai pensé qu'il fallait peut être calculer les coordonnées des vecteurs BA, AC, BC
AB ( -1; -1 ); AC ( 4; -2); BC ( 5; -1 );
et puis

Merci d'avance pour m'éclairer d'avantage sur la méthode à aborder pour réaliser cette exercice.

[capitaine nuggets]

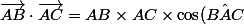salut !

bonjour a tous, je suis face à un exercice qui me pose beaucoup de problèmes.... je pense avoir compris la question posée mais je ne sais pas par ou commencer....

énoncé:

Dans un repère orthonormé, on donne les points (0 ; 2), (;)1 ; 1) et (4 ; 0).
Calculer au dixième près la mesure de l’angle ;);).

Idées:

J'ai pensé qu'il fallait peut être calculer les coordonnées des vecteurs BA, AC, BC
AB ( -1; -1 ); AC ( 4; -2); BC ( 5; -1 );
et puis

Merci d'avance pour m'éclairer d'avantage sur la méthode à aborder pour réaliser cette exercice.

Utilise la formule .

[paquito]

Tu as les coordonnées de AB et AC, donc tu peut calculer AB.AC, AB et AC et appliquer la formule qu'on
vient de te rappeler où cos(AB; AC) sera la seule inconnue.
Si tu as géogébra, tu peux vérifier très rapidement ton résultat.

[pbongrand]

soit (vecteur)AB.AC (vecteur) = xx'+yy'
= (-1) x 4 + 1 x (-2)
= (-4) + (-2)
=(-6)

Maintenant j'utilise la formule de captain nuggets
et je trouve -6= 1x 4 x cos(AB; AC)
cos(AB; AC) = -6 - 4= -10

[capitaine nuggets]

soit (vecteur)AB.AC (vecteur) = xx'+yy'
= (-1) x 4 + 1 x (-2)
= (-4) + (-2)
=(-6)

Maintenant j'utilise la formule de captain nuggets
et je trouve -6= 1x 4 x cos(AB; AC)
cos(AB; AC) = -6 - 4= -10

Sachant que, quel que soit l'angle , , ca va être dur de trouver un tel vérifiant :lol3:

Quelles sont les coordonnées des vecteurs et ?
Que valent les longueurs et ?
Enfin, attention, à ne pas confondre addition et multiplication :++:

[pbongrand]

les coordonnées des vecteurs AB et AC sont les suivantes

AB ( -1; -1) ; et AC ( 4; -2) soit (2; -1) (si je ne me trompes pas)

AB = -1; et AC = 4 (ou 2)

est ce que c'est correct ?

[pbongrand]

soit (vecteur)AB.AC (vecteur) = xx'+yy'
= (-1) x 2 + (-1) x (-1)
= (-2) + 1
=(-1)

Maintenant j'utilise la formule de captain nuggets
et je trouve -1= (-1)x 2 x cos(AB; AC)
(-1)= (-2) x cos(AB; AC)
(-1) / 2 = cos(AB; AC)= -0,5

[capitaine nuggets]

les coordonnées des vecteurs AB et AC sont les suivantes

AB ( -1; -1) ; et AC ( 4; -2) soit (2; -1) (si je ne me trompes pas)

AB = -1; et AC = 4 (ou 2)

est ce que c'est correct ?

AB est un longueur... comment pourrait-elle être négative ?
As-tu déjà tracer un segment de -2 cm ?

[paquito]

les coordonnées des vecteurs AB et AC sont les suivantes

AB ( -1; -1) ; et AC ( 4; -2) soit (2; -1) (si je ne me trompes pas)

AB = -1; et AC = 4 (ou 2)

est ce que c'est correct ?

Ac(4; -2), point final!
AB=V((-1)²+(-1)²)=V2.

[pbongrand]

Paquito:
pourquoi est ce qu'il y'a des ^2 dans l'expressions suivante:
AB=V((-1)²+(-1)²)=V2.

calcul:

soit (vecteur)AB.AC (vecteur) = xx'+yy'
= (-1) x 4 + (-1) x (-2)
= (-4) + 2
=(-2)

Maintenant j'utilise la formule de captain nuggets
et je trouve -2= 4x ;)2 x cos(AB; AC)
(-2)= 4;)2 x cos(AB; AC)
(-1) /(-4;)2) = cos(AB; AC)=1 /(4;)2)

vérification de l'encadrement de l'angle:

;)2 = 1,41 soir 4x 1,41 = 5,64

est cos(5,64) = 0,80018= 80°

[pbongrand]

est ce que c'est correct ?

[paquito]

Non, tu ne sait pas calculer la normr(longueur) d'un vecteur: c'est V(x²+y²) et c'est un résultat fondamental du cours.
Exemple: AC(4; -2), donc AC=V(4²+(-2)²)=V(20)!

[pbongrand]

ah merci (j'avais oublié...)

Soit AC= V(20) et AB= V2

Maintenant je réutilise la formule de captain nuggets
et je trouve -2= ;)20 x ;)2 x cos(AB; AC)
(-2)= 2;)10 x cos(AB; AC)
(-2) /(2;)10) = cos(AB; AC)=(-2) /(2;)10)

vérification de l'encadrement de l'angle:

(-2) /(2;)10) = -0,31622

est cos(-0,31622) = 0,950415= 95,0°

[paquito]

-2/2V10, ce n'est pas l'angle, mais son cos, donc fais cos^-1(-2/2V10) pour avoir ton résultat!
Rmq:-2/(2V10)=-1/V10.

[pbongrand]

soit cos^-1(-2/2V10)= 0,9875 soit l'angle est de 98,7°

[paquito]

soit cos^-1(-2/2V10)= 0,9875 soit l'angle est de 98,7°

Tu as encore réussi à te tromper! En plus regarde si tu es en mode degré ou radians.

[pbongrand]

je ne comprends pas où est l'erreur ? car j'ai recopié ce que tu avais précédemment écrit. avec le cos^-1(-2/2V10).

[paquito]

En mode radians arccos(-1/V10)=1,8925......en mode degré, 108,4349; résultat confirmé sur géogébra;
donc, je ne sais pas ce que tu fabriques! Il faut taper 2ndecos(-1/V10). Essaie encore...

[pbongrand]

Je ne sais pas si je dois donner l'angle en degrés ou en radians j'ai donc donner les deux résulats que je trouve:

Mode degrés:
j'ai taper 2ncos(-1/;)10); le résultat est 101,168671 soit un angle de 101,2 °

Mode radian:
j'ai taper 2ncos(-1/;)10); le résultat est 96,153716 soit un angle de 96,2 radians

Est ce que c'est correct ?

[paquito]

Je ne sais pas si je dois donner l'angle en degrés ou en radians j'ai donc donner les deux résulats que je trouve:

Mode degrés:
j'ai taper 2ncos(-1/;)10); le résultat est 101,168671 soit un angle de 101,2 °

Mode radian:
j'ai taper 2ncos(-1/;)10); le résultat est 96,153716 soit un angle de 96,2 radians

Est ce que c'est correct ?

2nde est parfois inv, donc tu dois taper peut être invcos pour avoir cos^-1 ou arccos; tant que tu n'auras pas les mêmes résultats que moi, tu auras fait une erreur de manipulation. recommence!