Exo Suite

[Jeremk57]

Bonjour,
Voila je bug sur un exercice sur les suites.

Soit la suite définie par=1 et ()=a+n+1
On suppose que a=0
Quelle est la nature de la suite?

J'ai un soucis avec cette question.

J'ai voulu déjà faire - ou / mais on ne connait pas Un
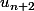
J'ai donc procédé avec et mais est ce que je peux ?
Ou alors en faite la suite n'est ni géométrique ni arithmétique.

Quelqu'un a une idée ?

Merci d'avance.

[Tiruxa]

Bonjour,
mais on ne connait pas Un

Mais oui tu as U(n+1) = n+1 pour tout entier n,

Donc en remplaçant n par n-1

U(n-1+1)=n-1+1 c'est à dire u(n) = n.

[Jeremk57]

Mais oui tu as U(n+1) = n+1 pour tout entier n,

Donc en remplaçant n par n-1

U(n-1+1)=n-1+1 c'est à dire u(n) = n.

Oui c'est ce que je pensais au début mais du coup si =n alors =0 et la sa ne colle plus avec l'énoncé... car =1

[paquito]

la suite est arithmétique à partir du rang n=1. Tu mets u(0) à part, c'est tout.

[Tiruxa]

Tu as raison, il aurait mieux valu prendre u0=0 dans l'énoncé.

Mais la formule U(n)=n est valable seulement à partir de n=1, car en remplaçant n (positif) par n-1, on doit avoir n-1 positif donc n supérieur à 1.

La suite est donc 1,1,2,3,4,5,6 etc....
On peut donc dire qu'lle est arithmétique à partir du terme de rang 1 (de u1 donc) et de raison 1, mais on peut aussi dire qu'elle n'est ni arithm ni géom si on la prend dans sa globalité.

[Jeremk57]

Tu as raison, il aurait mieux valu prendre u0=0 dans l'énoncé.

Mais la formule U(n)=n est valable seulement à partir de n=1, car en remplaçant n (positif) par n-1, on doit avoir n-1 positif donc n supérieur à 1.

La suite est donc 1,1,2,3,4,5,6 etc....
On peut donc dire qu'lle est arithmétique à partir du terme de rang 1 (de u1 donc) et de raison 1, mais on peut aussi dire qu'elle n'est ni arithm ni géom si on la prend dans sa globalité.

Oui je vois mieux là.
C'est logique
Merci