Dm la droite d'equation: (2m-1)X-my+3m+1=0
La droite Doest la droite obtenue pour m=0
Tracer la droite Do
Je trouve -X+1 mais ce n'est pas correct car elle ne se croise pas en un seul point avec D1,D2 et D-1.
Toutes lees autres sont correct sauf elle. :hein:
Merci de votre aide.
Equation de droite
11 messages
- Page 1 sur 1
BITW a écrit:Dm la droite d'equation: (2m-1)X-my+3m+1=0
La droite Doest la droite obtenue pour m=0
Tracer la droite Do
Je trouve -X+1 mais ce n'est pas correct car elle ne se croise pas en un seul point avec D1,D2 et D-1.
Toutes lees autres sont correct sauf elle. :hein:
Merci de votre aide.
Bonjour
Ne serais-ce pas la droite x=1( droite parrallele a l'axe des ordonnees)
BITW a écrit:Dm la droite d'equation: (2m-1)X-my+3m+1=0
La droite Doest la droite obtenue pour m=0
Tracer la droite Do
Je trouve -X+1 mais ce n'est pas correct car elle ne se croise pas en un seul point avec D1,D2 et D-1.
Toutes lees autres sont correct sauf elle. :hein:
Merci de votre aide.
"lle ne se croise pas en un seul point avec D1,D2 et D-1." formulation floue mais on devine la question : montrer que les droites
Il te faut trouver le point d'intersection de 2 droites
En faisant (1) - (2) qu'est-ce que tu observes ?
Carpate a écrit::
:
c'est la parallèle à l'axe des ordonnées passant par le point
"lle ne se croise pas en un seul point avec D1,D2 et D-1." formulation floue mais on devine la question : montrer que les droitespasse par un même point
Il te faut trouver le point d'intersection de 2 droites,
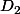
:
(1)
(2)
En faisant (1) - (2) qu'est-ce que tu observes ?
Euh, je dois soustraire?
D1 - D2?
je trouve 5X/2 + 15/2 :hein:
Carpate a écrit:n'est pas

Il te faut trouver le point d'intersection de 2 droites:
:
comme, le point d'intersection des droite
est, pour tout m, sur la droite d'équation
il est aussi sur
d'équation
, c'est donc le point
J'ai fais un systeme entre D1 et D2.
Je suis arrivé au meme resultat.
Merci de ton aide. :we:
BITW a écrit:h oui mains c'est pas bon ce que j'ai fais vu qu'il faut que ce soit vrai pour toute les droites dm.
Je vais appliquer ta technique.
Ma première méthode n'était pas tout à fait rigoureuse. En fait il faut montrer que la solution du système :
ne dépend pas de
Comme je suis flemmard, j'ai utilisé les formules de résolution d'un système de Cramer de 2 équations à 2 inconnues
Bonjour,
il me semble qu'il y a une méthode moins lourde en calculs :
On a :
(2m-1)X-my+3m+1=0
m(2x-y+3) -x+1=0
Pour que toutes les droites passent par un même point, il faut que leur équation ne dépende pas de m, donc que le terme en m soit nul, soit :
2x-y+3=0
On sait aussi que ces droites passent par x=1 pour qu'il y ait bien un point commun avec D0.
Donc :
2(1)-y+3=0
y=5
Donc le point commun a pour coordonnées (1,5)
il me semble qu'il y a une méthode moins lourde en calculs :
On a :
(2m-1)X-my+3m+1=0
m(2x-y+3) -x+1=0
Pour que toutes les droites passent par un même point, il faut que leur équation ne dépende pas de m, donc que le terme en m soit nul, soit :
2x-y+3=0
On sait aussi que ces droites passent par x=1 pour qu'il y ait bien un point commun avec D0.
Donc :
2(1)-y+3=0
y=5
Donc le point commun a pour coordonnées (1,5)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
