Rotation de deux masses.

[Anonyme]

Plus rien...

[XENSECP]

Tu veux pas faire le théorème des moments plutôt ?

Sinon tu appliques le pfd à quoi concrètement?

[Anonyme]

Re ,

Bonjour XENSECP, merci pour ta réponse,

A propos du moment cinétique, tu parles d'écrire :

avec J le moment cinétique, N le moment des forces.. ? Il me semble que c'est ce que j'ai essayé d'utiliser, à quoi concrètement ? Eh bien à la masse du bas par exemple.

J'écris le moment du poids comme étant : N = r x F = L/2*mg*sin(F, r). Après projection j'obtiens que le moment du poids est : N = -mgL/2*sin(théta).
L/2 est la distance de la boule du bas au centre de masse situé au milieu du fil.

Et là en faite j'ai du mal à exprimer le .. Puis-je écrire pour la masse du bas que j'étudie, que J = L/2*m*Vc.m (avec Vc.m, la vitesse du centre de masse) ?

Merci bien :lol3:.

[Anonyme]

Arf non j'ai beau le refaire j'arrive toujours à la même chose que dans mon post n°1.. Je pense que l'expression est correcte, seulement je n'arrive pas à faire apparaître Vc.m..

[Black Jack]

Je suppose que le "fil" est une barre rigide de masse quasi nulle.

I est je pense le moment d'inertie d'une masse par rapport à un axe passant par son centre.

Référentiel terrestre :
Il faut, je pense, prendre garde au fait qu'en plus du mouvement du centre d'inertie de la boule supérieure, les 2 boules tournent sur elle-même pendant le mouvement.

Penser à la lune qui montre toujours la même face vue de la Terre ... ce n'est pas parce la lune ne tourne par sur elle-même autour de son axe, mais bien parce que elle tourne sur elle même avec la même vitesse angulaire qu'elle ne tourne autour de la Terre...
Et dans le cas de l'exercice, on doit prendre en compte aussi cette rotation "sur elle-même" des 2 boules dans un bilan énergétique.

Référentiel terrestre :

Avec Theta0, l'angle de départ et wo la vitesse angulaire au départ.

Delta Ep = -mgL(cos(theta0) - cos(theta))

Delta Ec = 1/2 mL² (w²-wo²) + 2*1/2 * I(w²-wo²) = (w²-wo²).(I + mL²/2)

mgL(cos(theta0) - cos(theta)) = (w²-wo²).(I + mL²/2)

...

w = dtheta/dt = racinecarrée[(mgL.cos(theta0) + (I + mL²/2).wo² - mgL.cos(theta))/(I + mL²/2)]

Et le centre de masse a pour vitesse v = w.L/2

Et comme d'habitude, toutes erreurs incluses.

:zen:

[Anonyme]

Re Black Jack :),

Désolé je réponds à la bourre.. Merci pour le coup de main, je vais regarder ça de plus près, je te tiens au courant ;).

[Black Jack]

Re Black Jack ,

Désolé je réponds à la bourre.. Merci pour le coup de main, je vais regarder ça de plus près, je te tiens au courant .

Attention,

L'énoncé n'est pas clair par "deux masses de masse m possédant chacune un moment d'inertie égal à I"

L'énoncé ne précise pas de quel I il s'agit.

Moi, je l'ai considéré comme le moment d'inertie d'un masse par rapport à un axe passant par son centre d'inertie (celui de la masse).

Si l'énoncé voulait indiquer I comme le moment d'inertie d'une masse par rapport à un axe perpendiculaire au dessin et passant par le centre d'inertie de l'ensemble des 2 masses, alors ma réponse n'est évidemment pas celle attendue.

:zen:

[Anonyme]

Ah tu fais bien de le préciser.
Quand tu parle d'un à axe perpendiculaire, tu veux dire un axe z qui serait dirigé vers nous, et qui aurait comme origine le centre du fil ?

C'est en effet plus plausible que ce soit ça, mais je vais me renseigner.

Merci !

[Anonyme]

Re,

Ok alors voilà comment selon moi il faut voir les choses :

Moment d'inertie totale : (m(L/2)^2)*2

Moment cinétique : J = I;) = (m(L/2)^2)*2*;).

Moment des forces : = 2*mg*L/2*sin;) avec sin;) environ égal à , on obtient : = mg*L*;)

Je sais que dJ/dT = , donc de là j'arrive (sauf erreur) à : .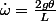

Je suis arrivé là par analogie avec un exercice "similaire", je le mets entre " " car ce n'est pas exactement la même chose.

Jusque là c'est bon ?

Vous allez me dire oui mais ça c'est et non pas 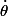que je recherche (cf. question initiale).. Eh bien vous avez raison . Le truc c'est que je ne vois toujours pas comment exprimé 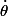, surtout en fonction de la vitesse du centre de masse..

Merci d'avance pour votre aide. :lol3:

P.S : Black Jack, selon moi du coup le premier raisonnement que tu as proposé n'est pas en accord avec l'exercice du coup.. A cause de ce que tu as écris dans le message suivant (selon moi).

[Black Jack]

Si I de l'énoncé est le moment d'inertie d'une masse par rapport à un axe perpendiculaire au dessin et passant par le centre d'inertie de l'ensemble des 2 masses, alors :

Avec Theta0, l'angle de départ et wo la vitesse angulaire au départ. (si wo = 0 et theta0 = 0, alors le machin reste immobile).

Ec = (1/2) * 2 * I * w² + (1/2)*2m*(Vc)²
Ec = I * w² + m*(Vc)²

Delta Ec = I * w² + m*(Vc)² - (I * wo² + m*(Vc0)²)
Delta Ec = I * (w²-wo²) + m*((Vc)² - Vco²)

Delta Ep = -mgL(cos(theta0) - cos(theta))

Delta Ec + Delta Ep = 0

I * (w²-wo²) + m*((Vc)² - Vco²) = mgL(cos(theta0) - cos(theta))

w² = Wo² + (mgL/I)(cos(theta0) - cos(theta)) - (m/I)*((Vc)² - Vco²)

Mais on a : Vc = w.L/2 et Vco = wo.L/2

w² = Wo² + (mgL/I).(cos(theta0) - cos(theta)) - m*L²/(4I) * (w² - wo²)

w²(1 + mL²/(4I)) = (mgL/I).(cos(theta0) - cos(theta)) + wo²(1 + mL²/(4I))

w² = wo² + [4mgL/(4I + mL²)] * (cos(theta0) - cos(theta))

Et dans le cas particulier où wo = 0 et que les 2 masses sont ponctuelles, alors I = mL²/4 et on retomberait sur :

w² = [4mgL/(mL² + mL²)] * (cos(theta0) - cos(theta))
w² = (2g/L) * (cos(theta0) - cos(theta))

... qui est aussi ce qu'on trouverait dans ma première réponse avec wo = 0 et I = 0 (ici I=0 à cause de la définition différente que j'avais prise de I).

*****

Si on repart de w² = wo² + [4mgL/(4I + mL²)] * (cos(theta0) - cos(theta))

en dérivant : 2w.dw/dt = [4mgL/(4I + mL²)].sin(theta).dtheta/dt

Mais w = dtheta/dt

Donc dtheta/dt = 0 est une solution (possible si accélération, et vitesse nulle, donc pour thta = 0 et theta = Pi/2 avec vitesse nulle).

Si w n'est pas identiquement nul alors --->

dw/dt = [2mgL/(4I + mL²)].sin(theta)

Et dans le cas particulier où les masses seraient ponctuelles, on aurait I = mL²/4
et dw/dt = (g/L).sin(theta) ... ce qui me semble juste puiqu'on est alors avec une masse sans inertie de rotation au sol ... et donc qui n'intervient plus.
et une masse motrice au bout d'une longueur L, --> couple moteur = mgL.sin(theta) et J total ici = mL²(seule masse du haut intervient dans ce cas extrème).
--> mgL.sin(theta) = mL².gamma (avec gamma l'acc angulaire)
gamma = g/L.sin(theta)

Sauf si je me trompe.

:zen:

[Anonyme]

Okay, ça marche, j'y vois un peu plus clair, merci bien pour le coup de main en tout cas ;).

A bientôt.